NYT Pips Hint, Answer & Solution for February 9, 2026

Feb 9, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

NYT Pips on Monday, February 9, 2026 is a structured logic workout designed for solvers who love clean constraints and efficient deductions.

Edited by Ian Livengood, today’s set scales up smoothly across three puzzles with clear data-driven progression.

Easy (ID 598): 5 dominoes, built around equals regions, empty cells, and tight <2 and >4 boundaries.

Medium (ID 627): 7 dominoes, featuring multiple sum=2 zones and a critical >9 region that quickly narrows viable placements.

Hard (ID 653): 15 dominoes, combining multiple sum targets (including 0-regions), a large unequal zone, and a final equals region that demands precise tracking.

If you’re chasing consistency and speed, this is a perfect puzzle day to test your logic, refine your grid scanning, and compare solution efficiency.

Written by Joe

Puzzle Analyst – Lucas

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - So easy

Just do it

💡 Hint #1 - Count the Bottleneck Pips

Strategy: Identify the rare pip value that every key region depends on. Key idea: only three dominoes contain a 2 pip half (3-2, 2-1, 2-0), but three separate “2” regions each require one. This means every 2-pip domino is already reserved, so placement order becomes a forced allocation problem.

💡 Hint #2 - Lock Equal Regions to Force the Layout

Strategy: Use Equal regions as anchors to fix high-value halves early. Key idea: Light Blue Equal can only be filled with 3s, and Blue Equal must be filled with 6s. Once those are locked, the only valid way to feed Top Purple 2 is to attach a 2 to the forced 3, and the remaining 6s naturally chain into the next placements.

💡 Hint #3 - Finish by Completing Required Pair Sums

Strategy: Close the puzzle by satisfying the last remaining totals with leftover dominoes. Key idea: Green >9 becomes forced into 5+5 once a 5 is already committed. Then Bottom Purple 2 must be 0+2, Yellow <2 must be 0+1, and the final unused 2 must slide into Red 2, completing the board through elimination.

💡 Hint #1 - Spot the Rare Numbers First

Strategy: Count the rare pips before placing anything. Key idea: only three dominoes contain 0, so the Number 0 region is highly restrictive and must be planned early. Also note Light Blue 2 is automatically forced into 1+1, and only (6-4) or (6-5) can create a >10 sum for the Purple 16 region.

💡 Hint #2 - Use Green 0 as the Main Anchor

Strategy: Use a forced region to lock the entire chain. Key idea: Green 0 guarantees a 0 pip half, which immediately controls the Light Blue Not Equal region. Once 0-0 is placed, the remaining cells must cover 1–6 without repeats, shrinking the options down to only two valid domino groupings.

💡 Hint #3 - Chain-Resolve the Forced Totals

Strategy: Solve clusters by satisfying multiple totals at once. Key idea: Purple 4 can only be completed by 2-2, and Yellow Equal must be a double (4-4 fits best). Then the remaining constraints force Red 6 into 3+3 and Blue >15 into three 6s, while Light Blue 2 stays locked as 1+1.

💡 Hint #4 - Eliminate to Lock Not-Equal Placement

Strategy: Let elimination finish the Not Equal region. Key idea: after the big totals consume most high values, the Light Blue Not Equal region has no flexibility left. The only way to avoid duplicates and satisfy the remaining pip coverage is to place 4-1 and 2-6 as the final confirmed pair.

💡 Hint #5 - Close the Puzzle with Leftover Math

Strategy: Use leftover sums to close the board cleanly. Key idea: Purple 16 becomes forced into 5+6+5, and Yellow 9 must be 5+2+2. With those totals locked, the remaining 0 halves naturally fill Red 0 and Blue 0, and Green Equal is forced to be 1 by elimination.

🎨 Pips Solver

Feb 9, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

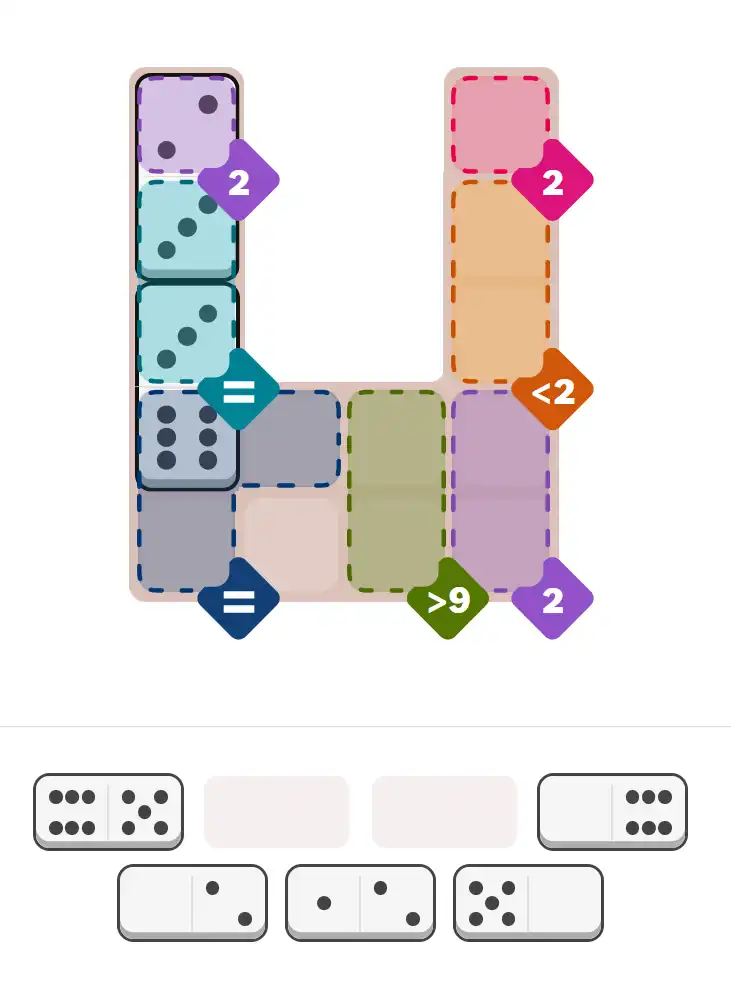
Starting Position & Key First Steps

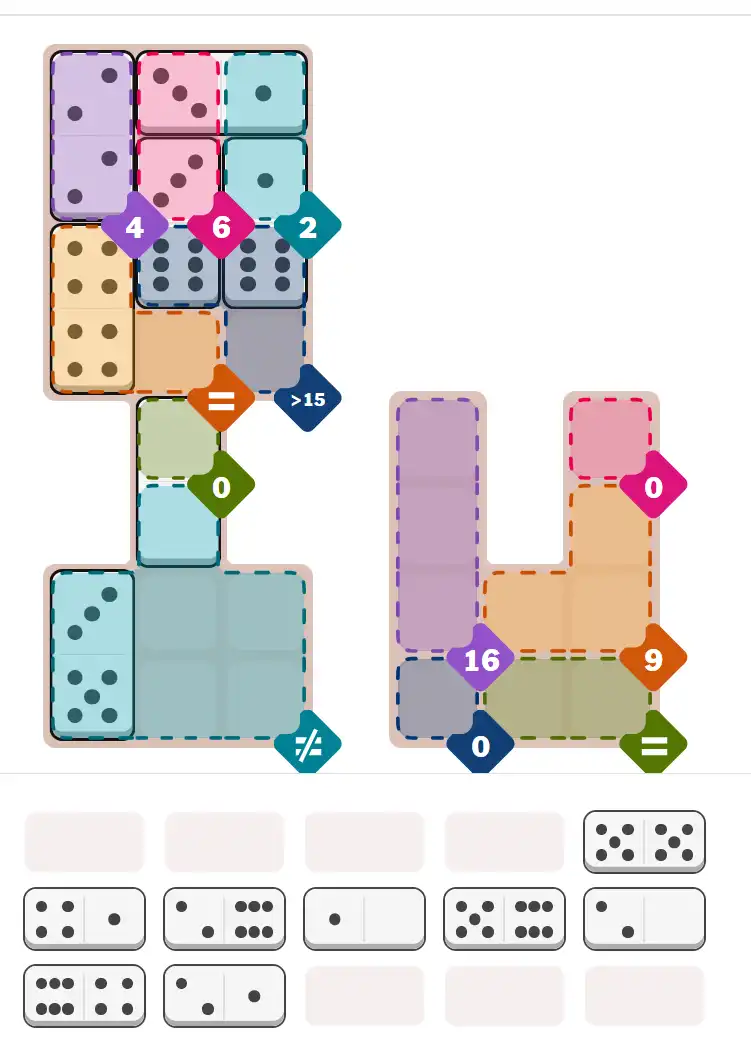
Pips hint for February 9, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

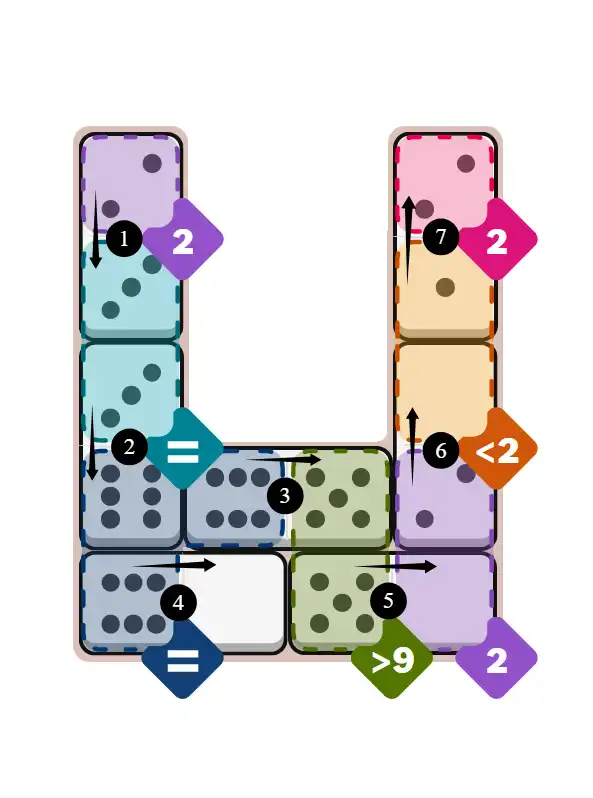
Final Answer: The Solved Grid for Hard Mode

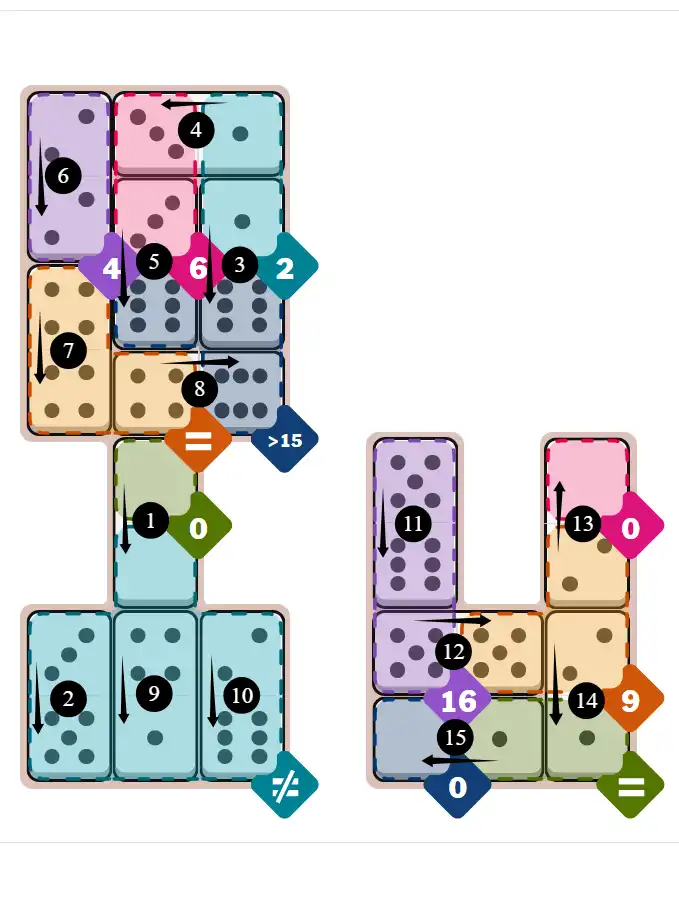
NYT Pips February 9, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-0], [5-4], [3-2], [1-1], [0-0].

2

Step 2: Red Equal --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Red Equal region must be 0. The answer is 0-0, placed vertically; 0-6 (6 down into blank), placed vertically.

3

Step 3: Purple <2 + Light Blue 8 + Yellow >4 --(Arrows ③④⑤)

Confirmed by neighboring region and remaining dominoes (5-4, 3-2, 1-1). The domino halves in Light Blue 8 region must be 1+4+3. The answer is 1-1 (one 1s into Purple <2 region), placed vertically; 5-4 (5 into Yellow >4 region), placed vertically; 3-2 (2 right into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-5], [6-3], [6-0], [5-0], [3-2], [2-1], [2-0]. Only 3 dominoes with 2 pips (3-2, 2-1, 2-0), need one for Top Purple 2 region, need one for Red 2 region, need one for Bottom Purple 2 region.

2

Step 2: Top Purple 2 + Light Blue Equal + Blue Equal --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Light Blue Equal region must be 3. The domino halves in Blue Equal region must be 6. The answer is 2-3 (2 into Top Purple 2 region), placed vertically; 3-6, placed vertically; 6-5 (5 into Green >9 region), placed horizontally; 6-0 (0 right into blank), placed horizontally.

3

Step 3: Green >9 + Bottom Purple 2 + Yellow <2 + Red 2 --(Arrows ⑤⑥⑦)

Confirmed by neighboring region and remaining dominoes (5-0, 2-1, 2-0). The domino halves in Green >9 region must be 5+5 (one 5s already come from Arrows ④). The domino halves in Bottom Purple 2 must be 0+2. The domino halves in Yellow <2 region must be 0+1. The answer is 5-0, placed horizontally; 2-0, placed vertically; 1-2 (2 into Red 2 region), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-5], [6-4], [6-3], [6-2], [6-1], [5-5], [5-3], [4-4], [4-1], [3-1], [2-2], [2-1], [2-0], [1-0], [0-0]. Only 3 dominoes with 0 pips (2-0, 1-0, 0-0) for Number 0 region. The domino halves in Light Blue 2 region must be 1+1. Only 3 dominoes with 3 pips (6-3, 5-3, 3-1). Need one domino sum to be more than 10 (6-4, 6-5) placed in Purple 16 region.

2

Step 2: Green 0 + Light Blue Not Equal --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. The domino halves in this region must be 0+1+2+3+4+5+6, need three whole dominoes placed in this region. The answer is 0-0 (one 0s into Green 0 region), placed vertically; 3-5 (whole domino), placed vertically. the other dominoes in Light Blue Not Equal region must be (6-4 and 2-1) or (6-2 and 4-1).

3

Step 3: Light Blue 2 + Red 6 + Purple 4 + Yellow Equal + Blue >15 --(Arrows ③④⑤⑥⑦⑧)

Confirmed by all left regions and remaining dominoes. Need one domino sum to be 4 (3-1, 2-2) placed in Purple 4 region. Need one domino with the same number (5-5, 4-4) placed in Yellow Equal region. The domino halves in Light Blue 2 region must be 1+1. The domino halves in Red 6 region must be 3+3. The domino halves in Yellow Equal region must be 4. The domino halves in Blue >15 region must be 6+6+6. The answer is 1-6, placed vertically; 1-3, placed horizontally; 3-6, placed vertically; 2-2 (whole domino into Purple 4 region), placed vertically; 4-4, placed vertically; 4-6, placed horizontally.

4

Step 4: Light Blue Not Equal --(Arrows ⑨⑩)

Confirmed by neighboring region and step 2 and remaining dominoes (6-5, 6-2, 5-5, 4-1, 2-1, 2-0, 1-0). The answer is 4-1, placed vertically; 2-6, placed vertically.

5

Step 5: Purple 16 + Yellow 9 + Red 0 + Green Equal + Blue 0 --(Arrows ⑪⑫⑬⑭⑮)

Confirmed by neighboring region and remaining dominoes (6-5, 5-5, 2-1, 2-0, 1-0). The domino halves in Purple 16 region must be 5+6+5. The domino halves in Yellow 9 region must be 5+2+2. The domino halves in Green Equal region must be 1. The answer is 5-6, placed vertically; 5-5, placed horizontally; 2-0 (0 into Red 0 region), placed vertically; 2-1, placed vertically; 1-0 (0 into Blue 0 region), placed horizontally.

🎥 NYT Pips Answers & Hints — February 9, 2026 (Monday) | Easy 598 • Medium 627 • Hard 653 Walkthrough

Drop your own solve time in the comments and share what deduction step helped you the most!

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for February 10, 2026

View Answer →

NYT Pips Hints & Answers for February 8, 2026

View Answer →

NYT Pips Hints & Answers for February 7, 2026

View Answer →

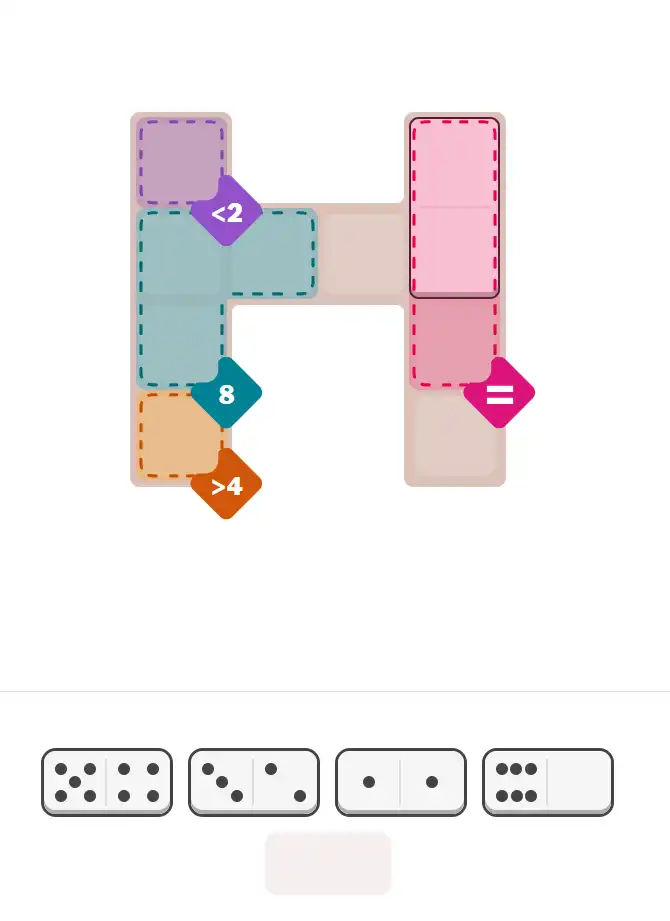
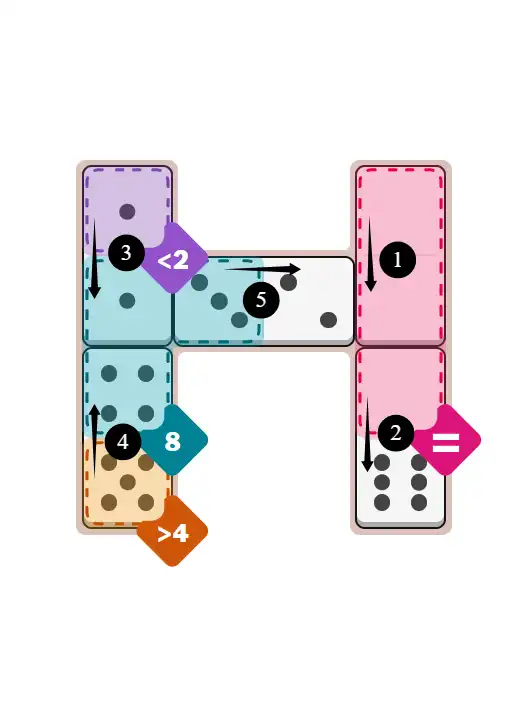
💬 Community Discussion

Leave your comment