NYT Pips Hint, Answer & Solution for February 10, 2026

Feb 10, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

NYT Pips for February 10, 2026 (Tuesday) is a clean logic test with escalating difficulty across three grids.

Edited by Ian Livengood, today’s puzzle set features sharp region math, forced equals placements, and domino constraints that reward precise counting.

📌 Easy Puzzle ID 605 uses 5 dominoes and pure sum targets (including 9, 11, and 4) for a fast warm-up.

📌 Medium Puzzle ID 634, constructed by Rodolfo Kurchan, adds 8 dominoes and multiple equals regions, plus a tight sum=1 block that heavily restricts placement.

📌 Hard Puzzle ID 660 pushes deeper with 12 dominoes, layered equals zones, sum requirements like 12 and 11, plus inequality regions (>2, <4, >4) that demand careful pip management.

If you're hunting for hints, logic breakdowns, or the full solution path, this walkthrough is built for accuracy and speed.

Written by Anna

Puzzle Analyst – Nikki

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - Nice and easy

Do it

💡 Hint #1 - Count Rare Zeros and Ones to Pre-lock the Light Blue 1 Region

Start by tracking pip scarcity: the Light Blue 1 region must total 0+0+0+1, but only three 0-halves and only two 1-halves exist. This immediately limits which dominoes can feed that region and also implies the 6 pip cannot be trapped there, so it must go into the blank space.

💡 Hint #2 - Use the Only 3-Pip Domino to Chain-Force All Equal Regions

Since [4-3] is the only domino containing a 3, Purple 4 can only be built as 1+3. That single decision cascades into forced values: Red Equal becomes 4, Yellow Equal becomes 2, and Green Equal becomes 5, letting you place multiple dominoes confidently without branching.

💡 Hint #3 - Complete Light Blue 1 by Filling the Remaining 0+0+1 Slots

After one 0 is already committed into Light Blue 1, the remaining requirement is still 0+0+1. With only (6-0, 2-2, 1-0) left, the 1 must come from 1-0 and the final 0s are forced, which also pushes the 6 downward into the last open blank.

💡 Hint #4 - Finish with the Only Remaining Double for the Equal Region

Once the other placements consume all alternatives, Blue Equal has only one valid match left. The remaining domino [2-2] satisfies the equal condition automatically, making it the clean forced endgame move.

💡 Hint #1 - Spot the Missing Number & Reserve Doubles Early

There is no 4-pip domino in the set, so any region that might normally rely on 4 must be solved through sums and forced pairs. Also, only three doubles exist (6-6, 5-5, 2-2), and two Equal regions require them—so plan your double allocation immediately.

💡 Hint #2 - Lock the Boundary Domino to Fix Multiple Regions

Use the Red 6 + Blue 4 boundary to force [3-2] into place, since it uniquely supports both targets. Once [3-2] is fixed, Blue 4 becomes 2+2 and Red Equal collapses to pip 1, which also helps confirm Purple 0 placement.

💡 Hint #3 - Use Equal Regions to Consume Rare Pips

Equal constraints quickly burn scarce high-value pips: Yellow Equal must take 5 (forcing 5-5), while Blue Equal must take 0. At the same time, Light Blue 12 demands double sixes, so 6-6 becomes unavoidable once one 6 is already committed.

💡 Hint #4 - Track the Last 5-Pip Half to Force the 11 Region

Light Blue 11 must be 5+6, but only one remaining domino contains a 5 half—so the 5 is locked. That immediately forces Yellow 6 to become 6+0, and the leftover 3 can be pushed into Green >2 via the only fitting option.

💡 Hint #5 - Finish the Remaining Equal Slot with the Only Double Left

After 6-6 and 5-5 are already used, the only double still available is 2-2. Since Purple Equal still needs a same-number domino, 2-2 becomes the forced final placement.

💡 Hint #6 - Resolve the Endgame with Inequality Direction

With only 3-6 left, inequality regions decide orientation: Green <4 must take the 3, and Purple >4 must take the 6. This guarantees the final placement without additional guessing.

🎨 Pips Solver

Feb 10, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

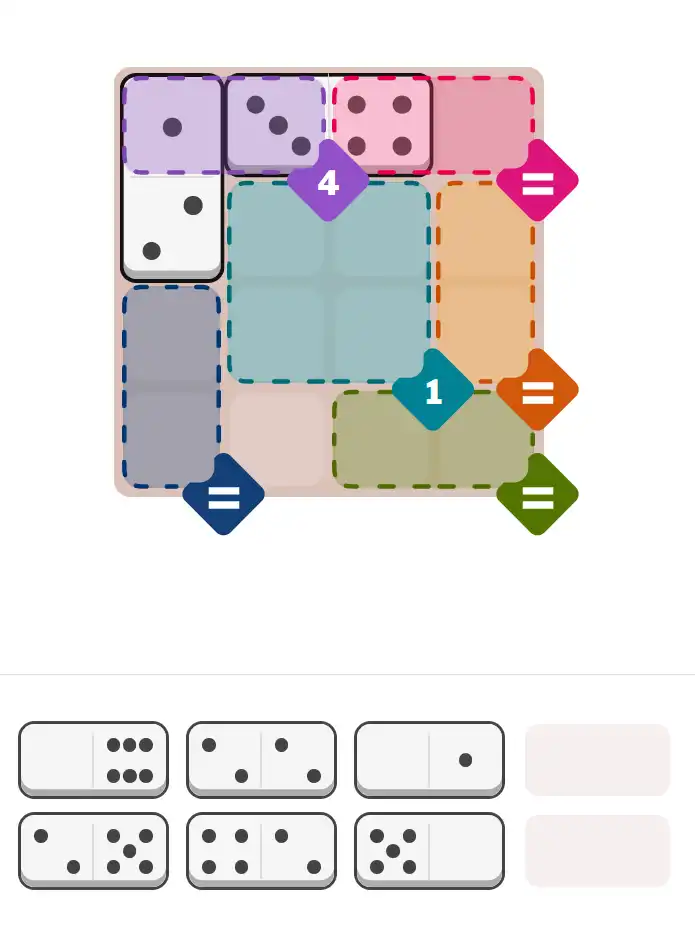
Starting Position & Key First Steps

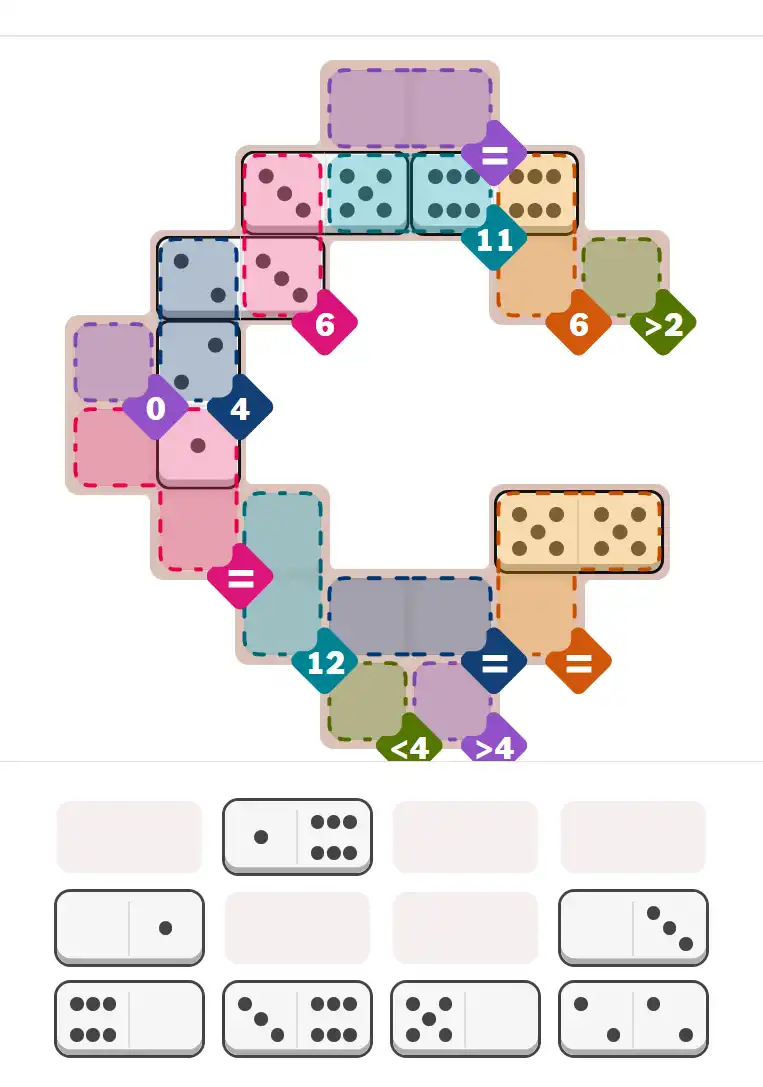
Pips hint for February 10, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

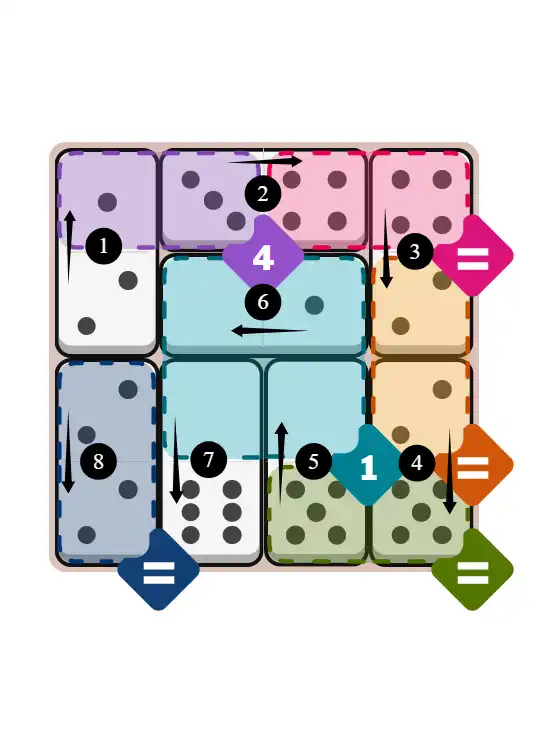
Final Answer: The Solved Grid for Hard Mode

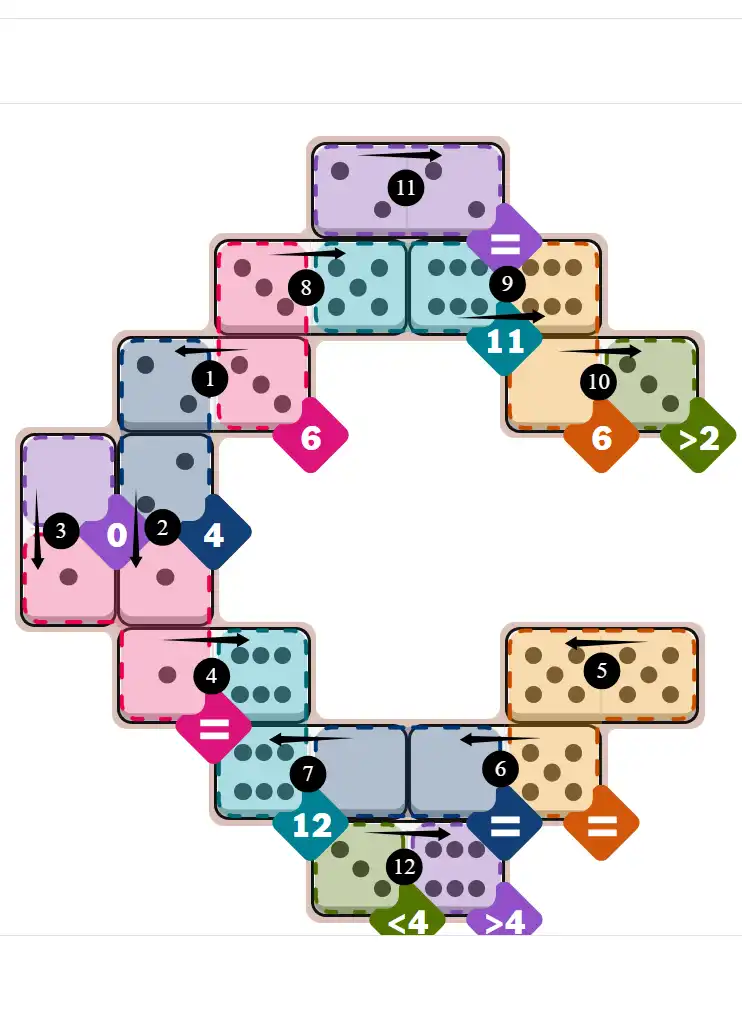
NYT Pips February 10, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-5], [5-2], [4-1], [3-2], [1-1].

2

Step 2: Blue 2 + Light Blue 11 + Purple 9 + Red 3 + Yellow 4 --(Arrows ①②③④⑤)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Light Blue 11 region must be 5+6. The domino halves in Purple 9 region must be 5+4. The domino halves in Red 3 region must be 1+2. The domino halves in Yellow 4 region must be 3+1. The answer is 2-5 (2 into Blue 2 region), placed horizontally; 6-5, placed horizontally; 4-1, placed horizontally; 2-3, placed horizontally; 1-1 (one 1s right into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-0], [5-2], [5-0], [4-3], [4-2], [2-2], [2-1], [1-0]. The domino halves in Light Blue 1 region must be 0+0+0+1. Only 3 domino halves that contain 0 pips (6-0, 5-0, 1-0). Only 2 domino halves that contain 1 pips (2-1, 1-0), need one for Light Blue 1 region. 6 pips must placed in blank.

2

Step 2: Purple 4 + Red Equal + Yellow Equal + Green Equal --(Arrows ①②③④⑤)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 3 pips (4-3). Therefore, the domino halves in Purple 4 region must be 1+3, the domino halves in Red Equal region must be 4, the domino halves in Yellow Equal must be 2, the domino halves in Green Equal region must be 5. The answer is 2-1 (2 into blank), placed vertically; 3-4, placed horizontally; 4-2, placed vertically; 2-5, placed vertically; 5-0 (0 into Light Blue 1 region), placed vertically.

3

Step 3: Light Blue 1 --(Arrows ⑥⑦)

Confirmed by neighboring region and remaining dominoes (6-0, 2-2, 1-0). The domino halves in Light Blue 1 region must be 0+0+0+1 (one 0s already come from Arrows ⑤). The answer is 1-0, placed horizontally; 0-6 (6 down into blank), placed vertically.

4

Step 4: Blue Equal --(Arrows ⑧)

The answer is 2-2, placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-6], [6-3], [6-1], [6-0], [5-5], [5-3], [5-0], [3-2], [3-0], [2-2], [2-1], [1-0]. No domino with 4 pips. Only 3 dominoes with the same number (6-6, 5-5, 2-2), need one for Yellow Equal region, need one for Purple Equal region. Only 5 domino halves that contain 6 pips, need two for Light Blue 12 region, need one for Light Blue 11 region. Only 4 domino halves that contain 5 pips, need one for Light Blue 11 region.

2

Step 2: Red 6 + Blue 4 + Purple 0 + Red Equal --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. [3-2] must placed in the boundary between Red 6 region and Blue 4 region. The domino halves in Red region must be 3+3 (one 3s come from step 4). The domino halves in Blue 4 region must be 2+2. The domino halves in Red Equal region must be 1. The answer is 3-2, placed horizontally; 2-1, placed vertically; 0-1 (0 into Purple 0 region), placed vertically; 1-6 (6 into Light Blue 12 region), placed horizontally.

3

Step 3: Yellow Equal + Blue Equal + Light Blue 12 --(Arrows ⑤⑥⑦)

Confirmed by all left regions and remaining dominoes (6-6, 6-3, 6-0, 5-5, 5-3, 5-0, 3-0, 2-2). The domino halves in Yellow Equal region must be 5. The domino halves in Blue Equal region must be 0. The domino halves in Light Blue 12 region must be 6+6 (one 6s already come from Arrows ④). The answer is 5-5, placed horizontally; 5-0, placed horizontally; 0-6, placed horizontally.

4

Step 4: Red 6 + Light Blue 11 + Yellow 6 + Green >2 --(Arrows ⑧⑨⑩)

Confirmed by neighboring region and remaining dominoes (6-6, 6-3, 5-3, 3-0, 2-2). The domino halves in Light Blue 11 must be 5+6. Only one domino left that contain 5 pips (5-3), so the domino halves in Yellow 6 region must be 6+0. The answer is 3-5 (3 into Red 6 region), placed horizontally; 6-6, placed horizontally; 0-3 (3 into Green >2 region), placed horizontally.

5

Step 5: Purple Equal --(Arrows ⑪)

Confirmed by neighboring region and remaining dominoes (6-3, 2-2). The answer is 2-2, placed horizontally.

6

Step 6: Green <4 + Purple >4 --(Arrows ⑫)

The answer is 3-6 (3 into Green <4 region, 6 into Purple >4 region), placed horizontally.

🎥 NYT Pips February 10, 2026 (Tuesday) — Full Solution Walkthrough for Easy 605 / Medium 634 / Hard 660

This video shows the key deductions without wasting time

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for February 9, 2026

View Answer →

NYT Pips Hints & Answers for February 8, 2026

View Answer →

NYT Pips Hints & Answers for February 7, 2026

View Answer →

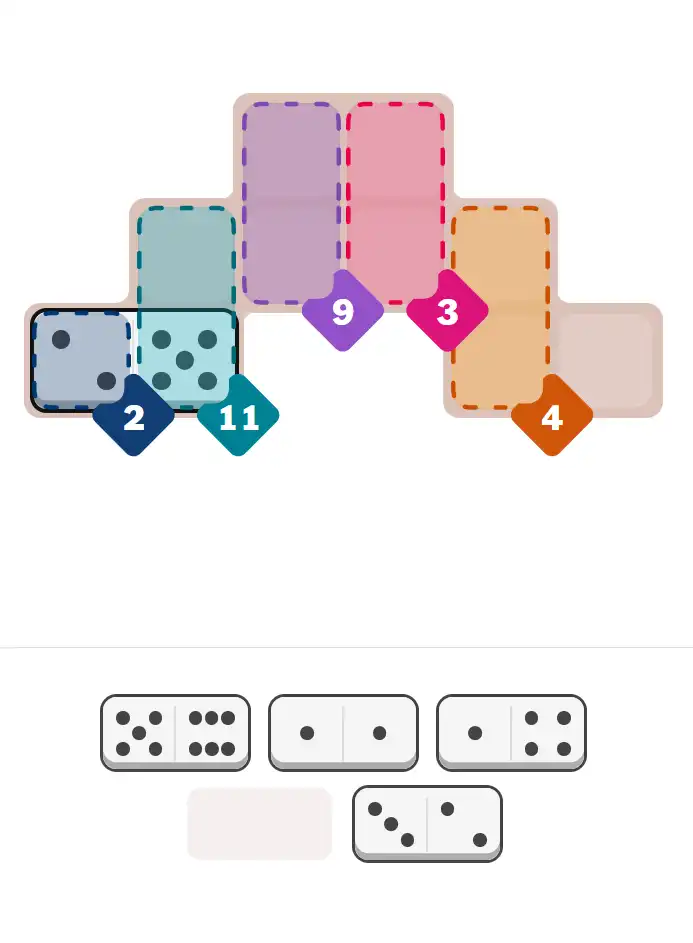
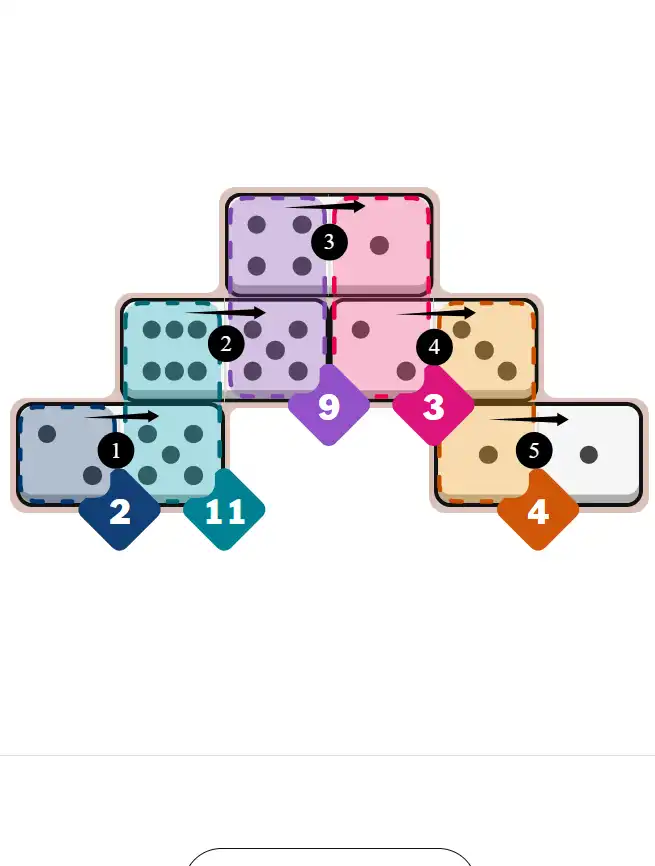
💬 Community Discussion

Leave your comment