NYT Pips Hint, Answer & Solution for February 7, 2026

Feb 7, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Saturday, February 7, 2026 brings a bold NYT Pips weekend lineup that feels perfect for solvers who love clean math, fast eliminations, and sharing sharp Pips hints with the community.

Edited by Ian Livengood, today’s set has a crisp “numbers-first” personality across all three difficulties, making it an ideal day to compare solution paths and trade that satisfying pips hint today moment when one placement unlocks the whole grid.

The easy puzzle (ID 590), created by Ian Livengood, is a pure power puzzle—just 4 dominoes, but a massive sum-30 region that forces immediate structure.

With extra <1 and <3 constraints plus a >3 check, it’s the kind of grid where the right first deduction feels instant.

The medium puzzle (ID 619) keeps the logic pressure steady, mixing multiple sum-7 regions, stacked equals zones, and a strict <2 region that cuts down possibilities fast.

If you enjoy tracking domino distribution and spotting forced pairs, this one delivers nonstop hint-worthy deductions.

The hard puzzle (ID 645) by Rodolfo Kurchan is a true weekend logic workout, built entirely around sum regions (from 2 up to 11) that chain together like a mathematical story.

Every placement matters, and every correct move creates a new opening.

If you’re searching for NYT Pips hints, a full solution walkthrough, or a clean strategy guide for February 7, 2026, this Saturday set is built for clarity, community discussion, and satisfying logic wins.

Written by Anna

Puzzle Analyst – Mark

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - So easy

Just do it

💡 Hint #1 - Spot the Forced Equal Number First

Before chasing sums, check the Equal regions and identify which pip value is most constrained. With multiple 4-heavy dominoes available and the layout demanding consistency, the Purple Equal region quickly locks onto 4 as the only stable option, narrowing the entire domino pool immediately.

💡 Hint #2 - Solve High-Value Sums Using Unique Pair Equations

Treat sum regions like equations and look for totals that only have one realistic pairing. Yellow 7 becomes 6+1, Blue 7 becomes 4+3, and once those pairs are identified, domino placement becomes straightforward because the remaining halves can’t realistically form the same totals.

💡 Hint #3 - Use the Equal Region as a Midgame Anchor

When a region requires identical numbers, scan the remaining set for the only double domino. Here, Red Equal instantly forces the 1-1 placement, which acts like a stabilizer and prevents wasted trial paths later.

💡 Hint #4 - Finish by Eliminating the Last Missing Pip

In the endgame, focus on what value the grid still needs rather than what it could take. Red <2 demands a 0 and a 1, which forces the 4-0 domino into position. With Purple Equal already locked on 4, the remaining 4-4 and 5-4 placements become automatic cleanup moves.

💡 Hint #1 - Count Critical Digits Before You Place Anything

Start by inventorying rare pip values and matching them to mandatory regions. Here, 6 appears only once (so Red 11 is basically forced), while 5-pips are heavily demanded across Yellow 10, Red 11, and Yellow 9. This kind of pip shortage immediately tells you which totals are locked and which regions will collapse first.

💡 Hint #2 - Use Shared Pip Bottlenecks to Solve Two Regions at Once

When two sum regions both require the same scarce number, treat them as linked. Blue 7 must be 4+3 and Purple 4 must be 1+3, but there are only two available 3-pip halves total. That means the 3s are automatically reserved for these regions, letting you place dominoes confidently without needing extra confirmation.

💡 Hint #3 - Lock Big Sums by Forcing the Only Valid Pairings

Once a key digit is already used (like the 4 placed into Light Blue 6), the remaining sums become rigid equations. Light Blue 6 becomes 4+2, Yellow 10 becomes 5+5, Red 11 becomes 6+5, and Yellow 9 becomes 5+4. This is a classic NYT Pips pattern: high totals often reduce to one legal pairing when pip counts are limited.

💡 Hint #4 - Finish the Grid by Solving the Leftover Domino Set

After the main sum regions are fixed, shift into cleanup mode: look at what dominoes remain and force their only possible homes. With only [4-4], [4-2], [4-1], and [1-1] left, the sums become unavoidable—Light Blue 8 must be 4+4, Purple 5 must be 4+1, and Red 3 must be 1+2. Endgame Pips is usually about leftover logic, not new discovery.

💡 Hint #5 - Use the Final Single Domino as a Placement Anchor

When only one domino can satisfy a small isolated region, place it immediately to stabilize the board. Green 2 has no flexibility here, so [1-1] becomes the natural final anchor placement. In NYT Pips, small sum regions often act as end-of-solve confirmation points.

🎨 Pips Solver

Feb 7, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

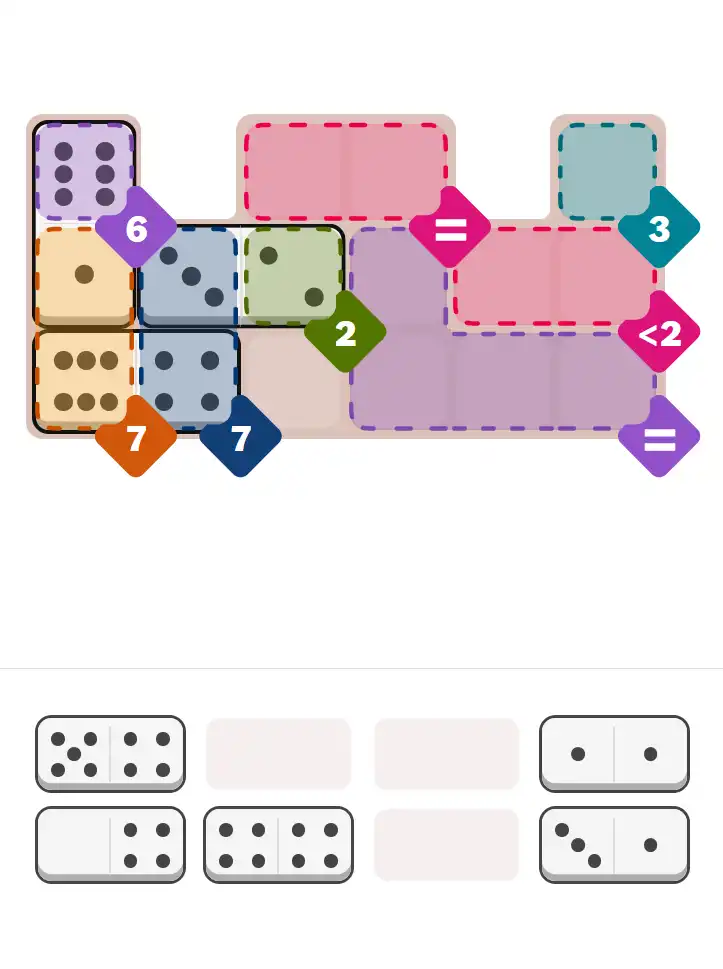
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

Starting Position & Key First Steps

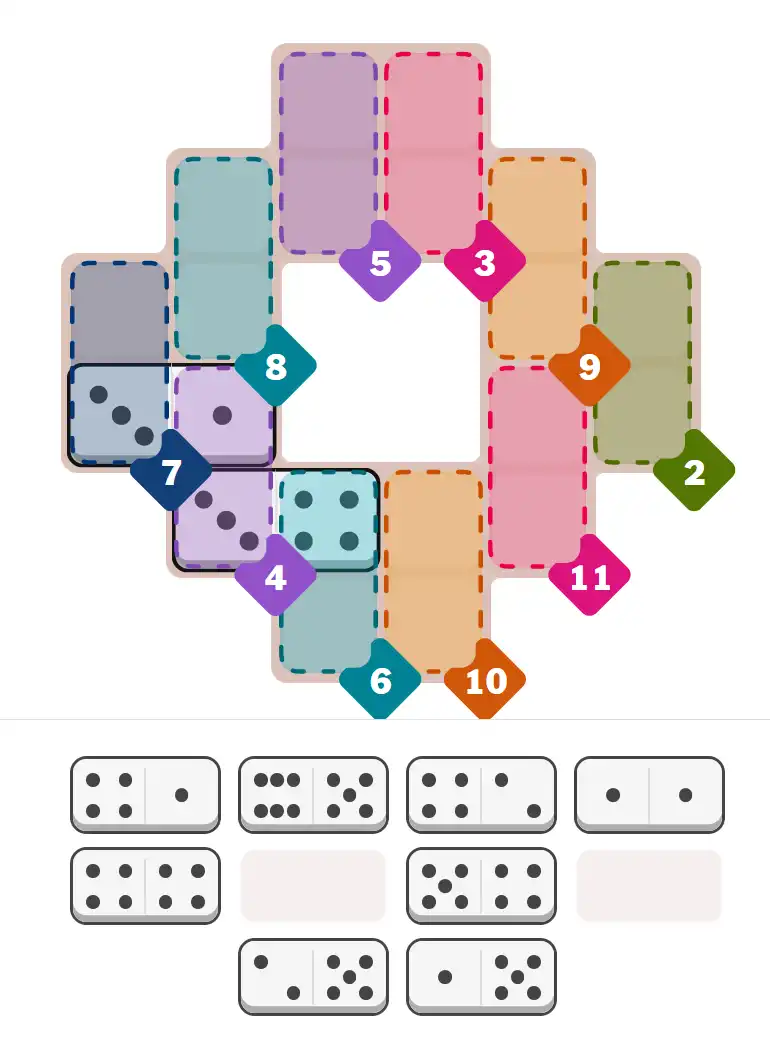
Pips hint for February 7, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

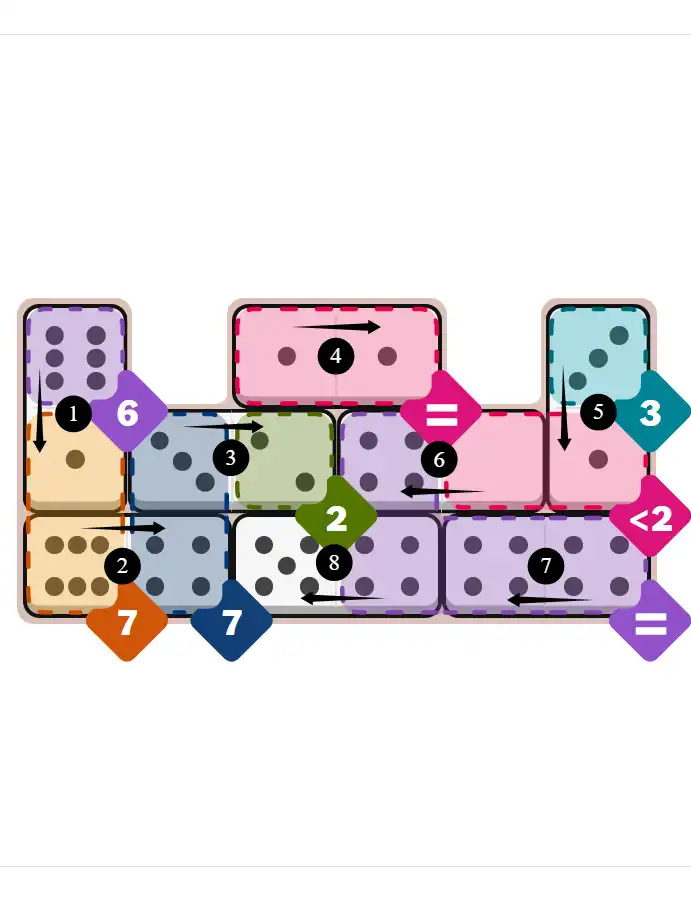
Final Answer: The Solved Grid for Hard Mode

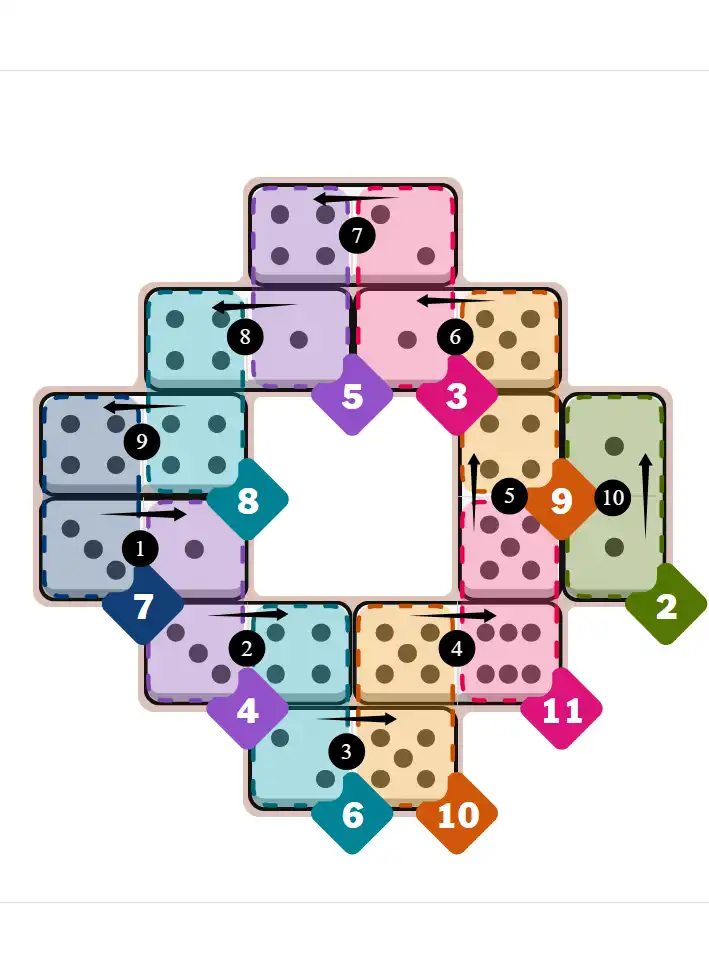
NYT Pips February 7, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-6], [6-4], [6-2], [6-0].

2

Step 2: Purple 30 + Light Blue <1 + Yellow <3 + Red >3 --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Purple 30 region must be 6+6+6+6+6. The answer is 6-6, placed horizontally; 6-0 (0 into Light Blue <1 region), placed horizontally; 6-2 (2 into Yellow <3 region), placed horizontally; 6-4 (4 into Red >3 region), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-4], [6-1], [5-4], [4-4], [4-0], [3-2], [3-1], [1-1]. The domino halves in Purple Equal region must be 4.

2

Step 2: Purple 6 + Yellow 7 + Blue 7 + Green 2 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Yellow 7 region must be 1+6. The domino halves in Blue 7 region must be 4+3. The answer is 6-1 (6 into Purple 6 region), placed vertically; 6-4, placed horizontally; 3-2 (2 into Green 2 region), placed horizontally.

3

Step 3: Red Equal --(Arrows ④)

Confirmed by neighboring region and step 1 and remaining dominoes. Need one domino with the same number placed in this region. The answer is 1-1, placed horizontally.

4

Step 4: Light Blue 3 + Red <2 + Purple Equal --(Arrows ⑤⑥⑦⑧)

Confirmed by neighboring region and remaining dominoes (5-4, 4-4, 4-0, 3-1). The domino halves in Red <2 region must be 1+0. The domino halves in Purple Equal region must be 4. The answer is 3-1 (3 into Light Blue 3 region), placed vertically; 0-4, placed horizontally; 4-4, placed horizontally; 4-5 (5 left into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-5], [5-4], [5-2], [5-1], [4-4], [4-3], [4-2], [4-1], [3-1], [1-1]. Only 5 domino halves that contain 5 pips (6-5, 5-4, 5-2, 5-1), need two for Yellow 10 region, need one for Red 11 region, need one for Yellow 9 region. Only one domino half that contain 6 pips for Red 11 region. Only 2 domino halves that contain 2 pips (5-2, 4-2), need one for Red 3 region.

2

Step 2: Blue 7 + Purple 4 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Blue 7 region must be 4+3. The domino halves in Purple 4 region must be 1+3. Only 2 domino with 3 pips (4-3, 3-1) for these two regions. The answer is 3-1 (3 into Blue 7 region), placed horizontally; 3-4 (4 into Light Blue 6 region), placed horizontally.

3

Step 3: Light Blue 6 + Yellow 10 + Red 11 + Yellow 9 --(Arrows ③④⑤⑥)

Confirmed by neighboring region and step 1 and remaining dominoes. The domino halves in Light Blue 6 region must be 4+2 (4s already come from Arrows ②). The domino halves in Yellow 10 region must be 5+5. The domino halves in Red 11 region must be 6+5. The domino halves in Yellow 9 region must be 5+4. The answer is 2-5, placed horizontally; 5-6, placed horizontally; 5-4, placed vertically; 5-1 (1 into Red 3 region), placed horizontally.

4

Step 4: Red 3 + Purple 5 + Light Blue 8 --(Arrows ⑦⑧⑨)

Confirmed by neighboring region and remaining dominoes (4-4, 4-2, 4-1, 1-1). The domino halves in Red <2 region must be 1+0. The domino halves in Red 3 region must be 1+2 (1s already come from Arrows ⑥). The domino halves in Purple 5 region must be 4+1. The domino halves in Light Blue 8 region must be 4+4. The answer is 2-4, placed horizontally; 1-4, placed horizontally; 4-4 (one 4s into Blue 7 region, 3s already come from Arrows ①), placed horizontally.

5

Step 5: Green 2 --(Arrows ⑩)

The answer is 1-1, placed vertically.

🎥 NYT Pips Hint Today (Feb 7, 2026) — Full Solutions for Easy 590, Medium 619 & Hard 645

This video gives a clean, reliable solve path you can follow in real time.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for February 8, 2026

View Answer →

NYT Pips Hints & Answers for February 6, 2026

View Answer →

NYT Pips Hints & Answers for February 5, 2026

View Answer →

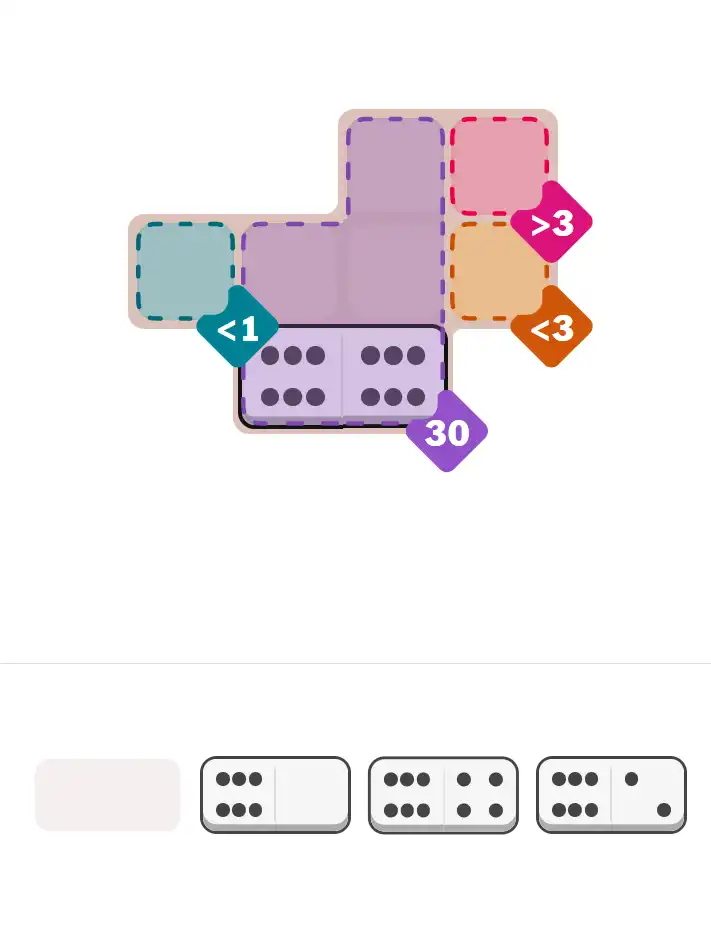
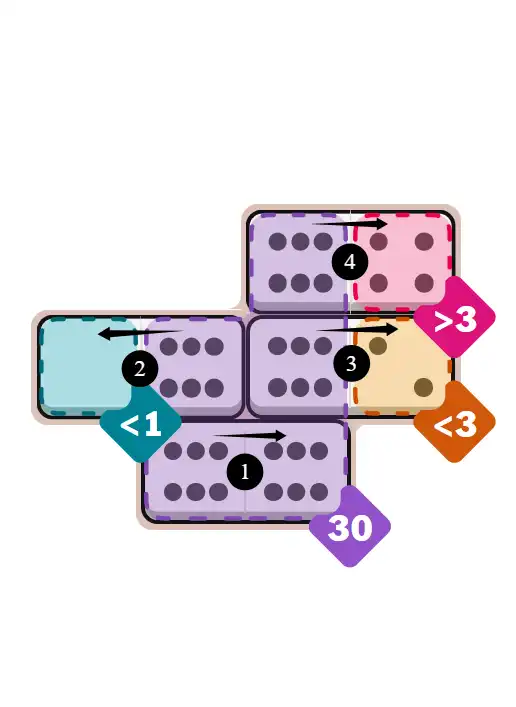
💬 Community Discussion

Leave your comment