🚨 SPOILER WARNING
This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!
Click here to play today's official NYT Pips game first.
Want hints instead? Scroll down for progressive clues that won't spoil the fun.
🎲 Today's Puzzle Overview
Saturday, November 29, 2025, arrives with a lively trio of Pips NYT puzzles—an ideal lineup for solvers who enjoy sharing ideas, comparing paths, and trading their favorite Pips Hints throughout the day.
Guided by editor Ian Livengood, today’s puzzles present three community-ready challenges:
Easy #360 by Ian Livengood, Medium #363 by Rodolfo Kurchan, and Hard #366, also crafted by Rodolfo.
The Easy puzzle sets a friendly tone with two empty starter cells, a clean sum-6 pairing, a compact sum-3 region, and a neat equals block that naturally inspires quick back-and-forth discussion.
Medium expands the conversation with a sharper mix of logic signals—a less-than-5 clue, multi-cell equals clusters, an 8-sum chain, plus several empty anchors that shape early strategies and invite players to ask, “Where did you begin?”
The Hard puzzle closes the set with rich, layered deduction: stacked equals structures, targeted greater-than-2 and greater-than-3 hints, and a dense, visually striking 17-sum run that rewards collaborative reasoning and community-powered solution analysis.
Whether you’re posting your grid, sharing the Pips Hint that cracked the puzzle open, or comparing how you navigated the constraint layout, November 29 offers a full day of puzzle conversation and shared breakthroughs.
A perfect Saturday for solvers who enjoy logic—and each other’s company.
Written by July
Puzzle Analyst – Mark
💡 Progressive Hints
Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!
💡 Hint #1 - So easy
Just do it.
💡 Hint #1 - Observe
Dominoes Include: [6-4], [6-0], [5-0], [4-0], [2-2], [2-0], [0-0]. The relative positions of dominoes can be inferred from each other. The domino halves in Red Equal region must be 0. A whole domino must placed in Yellow Number (8) region.
💡 Hint #2 - Yellow Number (8)
The domino halves in this region must be 4+2+2.
💡 Hint #1 - Step 1
Dominoes Include: [6-4], [6-3], [6-1], [5-2], [5-0], [4-0], [3-3], [3-2], [1-1], [1-0], [0-0]. Only 3 domino halves that contain 6 pips (6-4, 6-3, 6-1). Only 2 domino halves that contain 5 pips (5-2, 5-0). The domino halves in Green Number (17) region must be 6+6+5. The domino halves in Purple Greater Than (9) region must be 6+4 or 6+5. The domino has 5 or 6 on one end, then the other end is < 3. Only 5 domino halves that contain 0 pips (5-0, 4-0, 1-0, 0-0). Therefore, the domino halves in Yellow Equal region must be 0.
💡 Hint #2 - Step 2: Red Greater Than (3) + Green Number (17)+ Blue Greater Than (3) + Yellow Equal
Confirmed by neighboring region and step 1. The domino halves in Green Number (17) region must be 5+6+6. The domino halves in Yellow Equal region must be 0. The answer is 4-6, placed vertically; 5-0, placed vertically; 4-0, placed vertically; 0-0, placed horizontally.
💡 Hint #3 - Step 3: Purple Greater Than (9) + Red Equal
Confirmed by neighboring region and remaining dominoes. The domino halves in Purple Greater Than (9) region must be 5+6. The domino halves in Red Equal region must be 1 (confirmed by next the other regions). The answer is 2-5, placed vertically; 6-1, placed vertically; 0-1, placed vertically; 1-1, placed vertically.
💡 Hint #4 - Step 4: Light Blue Equal
Confirmed by neighboring region and remaining dominoes. The answer is 3-3, placed vertically.
💡 Hint #5 - Step 5: Green Number (17)
Confirmed by neighboring region and remaining dominoes. The answer is 6-3, placed vertically.
💡 Hint #6 - Step 6: Purple Greater Than (2)
The answer is 3-2, placed horizontally.
🎨 Pips Solver
Nov 29, 2025
Click a domino to place it on the board. You can also click the board, and the correct domino will appear.
✅ Final Answer & Complete Solution For Hard Level
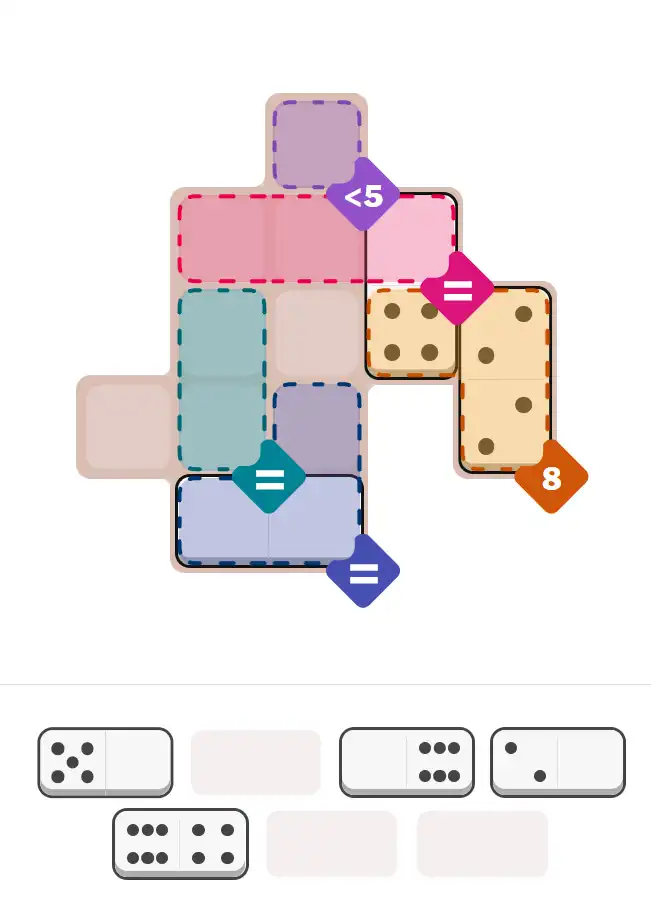
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.
Starting Position & Key First Steps
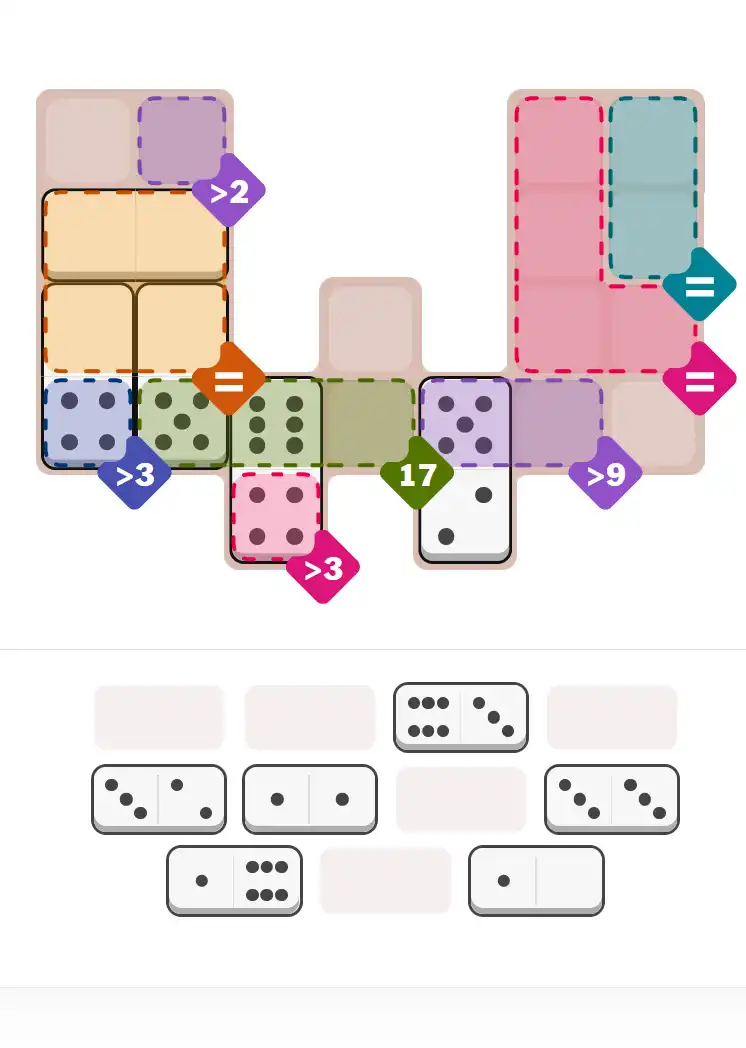
This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.
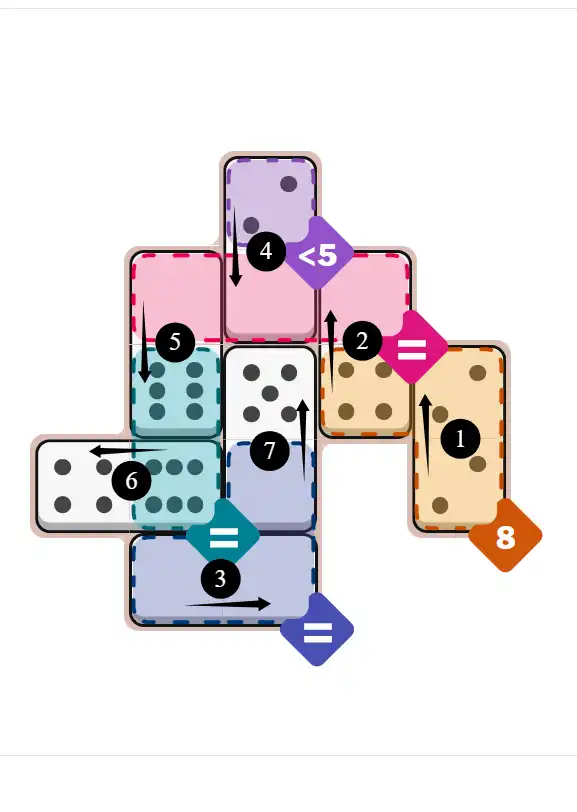
Final Answer: The Solved Grid for Hard Mode
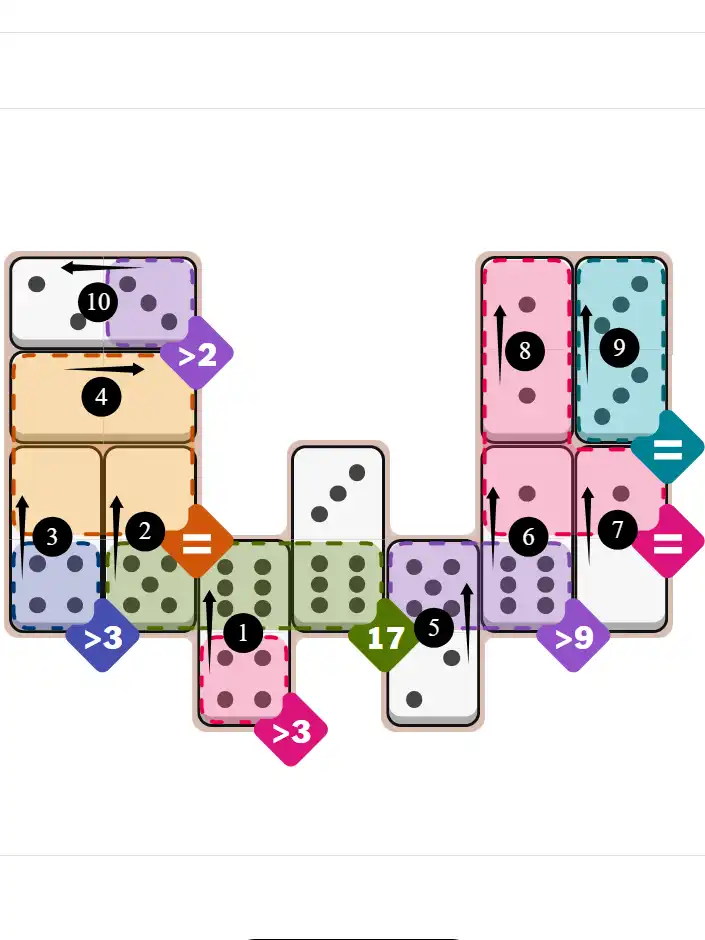
Compare this final grid with your own solution to see the correct placement of all dominoes.
🔧 Step-by-Step Answer Walkthrough For Easy Level
1
Step 1: Inventory Analysis - Limited Pieces, Strategic Placement
Dominoes: 6-2, 5-0, 4-3, 2-1. With only four dominoes available, this puzzle requires precise placement—every domino must serve its exact purpose. Looking at the board, we have multiple constraint regions: Yellow 6, Light Blue Equal, Purple 6, and Red 3. The key observation: Light Blue Equal region needs matching pip values, and checking our inventory, only one value appears in multiple dominoes—the 2 appears in both 6-2 and 2-1, giving us exactly two 2-halves. This predetermined allocation means Light Blue Equal MUST use these two 2s. Pips Hint: with limited dominoes, identify which constraint regions have only one mathematically possible solution—equal regions requiring matching pips often reveal themselves through inventory scarcity.
2
Step 2: Yellow 6 + Light Blue Equal + Purple 6 - Triple Constraint Solving
Three interconnected regions cluster together: Yellow 6 (bottom left), Light Blue Equal (center), and Purple 6 (right side). From Step 1, Light Blue Equal needs two 2-halves. Yellow 6 needs exactly 6. Purple 6 needs exactly 6. Let's solve systematically. Place 6-2 horizontally (6 in Yellow 6, 2 in Light Blue Equal). Place 2-1 horizontally (2 in Light Blue Equal, 1 in Purple 6). Light Blue Equal now has two matching 2s ✓. Yellow 6 receives 6 from one domino ✓. Purple 6 already has 1, needs 5 more (1+5=6). Place 5-0 horizontally (5 in Purple 6, 0 extends elsewhere). Purple 6: 1+5=6 ✓. This cascading placement demonstrates how one strategic decision (allocating both 2s to Light Blue Equal) determines the entire solution path for three regions simultaneously. Pips Hint: when equal regions consume specific pip values, track where those pips come from—the dominoes providing matching values to equal regions also position their partner halves into adjacent sum regions, creating natural solving cascades.
3
Step 3: Red Number 3 - The Final Piece
Final region: Red 3 (left side). Last domino remaining: 4-3. Red 3 needs exactly 3. Place 4-3 vertically (3 in Red 3 region, 4 extends into another area or blank space). Red 3: receives exactly 3 ✓. Puzzle complete with all four dominoes placed. This simple puzzle demonstrates a fundamental principle: when you have fewer dominoes than constraint regions, some regions must share domino halves—the art lies in determining which regions share which dominoes, guided by mathematical constraints like equal regions needing matching values. Step 1's identification of the two 2-halves for Light Blue Equal was the key that unlocked the entire solution. Pips Hint: in minimal-domino puzzles, the final piece always fits inevitably—if it doesn't, backtrack to your equal region allocations, as those predetermined placements are usually where errors occur.
🔧 Step-by-Step Answer Walkthrough For Medium Level
1
Step 1: Strategic Overview - Five 0-Bearing Dominoes and the Complete Domino Rule
Dominoes: 6-4, 6-0, 5-0, 4-0, 2-2, 2-0, 0-0. Critical observations: FIVE dominoes contain 0-pips (6-0, 5-0, 4-0, 2-0, 0-0), with 0-0 providing TWO 0-halves—giving us six 0-halves total. This concentration means Red Equal region must use 0s for its matching pattern. Additionally, Yellow 8 region needs exactly 8, with a unique constraint: a WHOLE domino (both halves) must be placed entirely within Yellow 8's boundary. The relative positioning of regions allows us to infer logical placements from each other—each number and placement has clear reasoning. Pips Hint: precisely count your pip inventory—'five dominoes with 0s' versus 'six 0-halves total' is a crucial distinction when planning equal-region allocations.
2
Step 2: Yellow Number 8 - The 4+2+2 Configuration
Yellow 8 region (right side) needs exactly 8. From Step 1, we need dominoes totaling 8. The answer confirms: 4+2+2=8. Place 2-2 vertically (both 2-halves entirely within Yellow 8). Place 4-0 vertically (4 in Yellow 8, 0 extends UPWARD into Red Equal region above). Yellow 8: 4+2+2=8 ✓. The 0 from 4-0 going upward into Red Equal is confirmed by the board layout—Red Equal sits above the Yellow region. Pips Hint: when placing dominoes in sum regions, track where partner halves extend—they often contribute to adjacent equal regions, creating natural solving cascades.
3
Step 3: Blue Equal Region - The 0-0 Foundation
From Step 2, we've allocated one 0 to Red Equal. Now Blue Equal region needs matching pips—it uses 0s. Place 0-0 horizontally (both 0-halves in Blue Equal region). Blue Equal now has two matching 0s ✓. This locks in one complete equal region. Remaining 0-bearing dominoes for other regions: 6-0, 5-0, 2-0. Pips Hint: placing double-zero (0-0) in equal regions is efficient—it instantly provides two matching cells while preserving other 0-bearing dominoes for regions needing diverse pip combinations.
4
Step 4: Purple Less-Than-5 + Red Equal + Light Blue Equal - Precise Triple Solution
Three regions require attention: Purple <5 (top center), Red Equal (horizontal center), Light Blue Equal (left). From Step 2, Red Equal already has one 0. Looking at the board carefully, Purple <5 needs a value less than 5. Remaining dominoes: 6-0, 5-0, 2-0, 6-4. The answer specifies: Place 2-0 vertically (2 in Purple <5 satisfying 2<5 ✓, 0 in Red Equal). Place 6-0 vertically (0 in Red Equal, 6 in Light Blue Equal). Place 6-4 horizontally (6 in Light Blue Equal, 4 extends elsewhere). Red Equal now has three matching 0s (from Step 2's 4-0, plus 2-0, plus 6-0) ✓. Light Blue Equal has two matching 6s ✓. Purple <5 receives 2 ✓. Every number placement has clear reasoning based on constraints. Pips Hint: when inequality regions neighbor equal regions, test which small values satisfy inequalities—2<5 works perfectly while positioning the 0 to serve Red Equal's matching requirement.
5
Step 5: Blue Equal Region - Final 0 Completion
Final domino: 5-0. Place 5-0 vertically (0 in Blue Equal region, 5 extends elsewhere). Blue Equal now complete with matching 0s ✓. Puzzle solved—all constraints satisfied with precise reasoning at every step. Step 1's accurate count (five 0-bearing dominoes with six 0-halves total) guided the entire solution, ensuring Red Equal and Blue Equal regions received exactly the 0s they needed. Pips Hint: final placements validate your entire pip-counting strategy—if the last domino fits perfectly, your Step 1 inventory analysis and every subsequent directional placement were logically sound and inevitable.
🔧 Step-by-Step Answer Walkthrough For Hard Level
1
Step 1: Comprehensive Inventory Analysis - High-Value Scarcity and 0-Pip Allocation
Dominoes: 6-4, 6-3, 6-1, 5-2, 5-0, 4-0, 3-3, 3-2, 1-1, 1-0, 0-0. Critical observations: Only 3 domino halves contain 6-pips (from 6-4, 6-3, 6-1). Only 2 domino halves contain 5-pips (from 5-2, 5-0). Green 17 region needs exactly 17—testing high-value combinations: 6+6+5=17 works perfectly. Purple >9 region needs values greater than 9—testing: 6+4=10 or 6+5=11 both work. Key constraint: if a domino has 5 or 6 on one end, the other end must be <3 (less than 3). Only 5 domino halves contain 0-pips (from 5-0, 4-0, 1-0, 0-0). Therefore, Yellow Equal region MUST use 0s—we have exactly enough 0-halves to fill it. This predetermined allocation of scarce high values (6s and 5s) and abundant 0s drives the entire solution. Pips Hint: when extreme sum regions like 17 exist alongside scarcity of high-value pips, calculate the ONLY viable combination first—this locks in which dominoes serve which regions before placing anything.
2
Step 2: Red >3 + Green 17 + Blue >3 + Yellow Equal - Quad-Region Foundation
Four interconnected regions form the puzzle's foundation: Red >3 (left side), Green 17 (center horizontal), Blue >3 (bottom left), and Yellow Equal (center horizontal). From Step 1, Green 17 needs 5+6+6=17. Yellow Equal needs all 0s. Place 6-4 vertically (6 in Green 17, 4 in Red >3 satisfying 4>3 ✓). Place 5-0 vertically (5 in Green 17, 0 in Yellow Equal). Place 4-0 vertically (4 in Blue >3 satisfying 4>3 ✓, 0 in Yellow Equal). Place 0-0 horizontally (both 0s in Yellow Equal). Green 17 now has: 6+5... needs one more 6 (to be completed in Step 5). Yellow Equal has four matching 0s ✓. Red >3 receives 4 ✓. Blue >3 receives 4 ✓. This cascading placement demonstrates how one region's extreme requirement (Green 17 needing 6+6+5) positions dominoes that simultaneously satisfy adjacent inequality and equal constraints. Pips Hint: when placing high-value dominoes in extreme sum regions, verify their partner halves satisfy adjacent constraints—dual-purpose placements are essential in complex puzzles.
3
Step 3: Purple >9 + Red Equal - High Values and 1s Strategy
Two regions require attention: Purple >9 (right side) and Red Equal (right vertical). From Step 1, Purple >9 needs values totaling more than 9—testing: 5+6=11 works (11>9 ✓). Red Equal needs matching pips throughout. Remaining dominoes with high values: 6-1, 5-2. Checking available matching values for Red Equal: we have 1-1, 6-1, 1-0, giving us four 1-halves—Red Equal MUST use 1s (confirmed by checking other regions' requirements). Place 5-2 vertically (5 in Purple >9, 2 extends elsewhere). Place 6-1 vertically (6 in Purple >9, 1 in Red Equal). Place 1-0 vertically (1 in Red Equal, 0 extends to blank). Place 1-1 vertically (both 1s in Red Equal). Purple >9: 5+6=11 ✓. Red Equal has four matching 1s ✓. The strategic insight: If the Red Equal region were to use 3s, there would be no remaining domino halves available to satisfy the other “>2” inequality regions (for example, the Purple >2 region). That would make it impossible to place any domino that meets the Purple >2 constraint. Therefore, by elimination and availability of remaining tiles, the Red Equal region must be filled with 1s. Pips Hint: when equal regions appear mid-puzzle, inventory remaining matching values—the region uses whichever value has exactly enough halves to fill all its cells.
4
Step 4: Light Blue Equal - The Double 3s
Light Blue Equal region (right side) needs matching pips. Remaining dominoes: 6-3, 3-3, 3-2. Checking which value works: we have three 3-halves (from 6-3, 3-3, 3-2). Light Blue needs matching 3s. Place 3-3 vertically (both 3s in Light Blue Equal). Light Blue Equal now has two matching 3s ✓. More 3s will come from subsequent steps if Light Blue spans more cells. Pips Hint: when placing double dominoes (like 3-3) in equal regions, they efficiently claim two cells instantly—prioritize doubles for equal constraints when region size permits.
5
Step 5: Green Number 17 - Completing the High-Value Sum
From Step 2, Green 17 already has 6+5 (totaling 11). It needs 6 more to reach 17. Remaining domino with 6: 6-3. Place 6-3 vertically (6 in Green 17, 3 in blank). Green 17 calculation: 6 (from Step 2's 6-4) + 5 (from Step 2's 5-0) + 6 (from this step's 6-3) = 17 ✓. Step 1's prediction validated—6+6+5 was indeed the only combination achieving 17 with our limited high-value inventory. Pips Hint: extreme sum regions often require multi-step completion—track partial sums carefully and verify the final domino provides exactly the remaining deficit.
6
Step 6: Purple Greater-Than-2 - The Final Constraint
Final region: Purple >2 (top left). Last domino remaining: 3-2. Purple >2 needs any value greater than 2. Place 3-2 horizontally (3 in Purple >2 satisfying 3>2 ✓, 2 extends elsewhere). Puzzle complete—all six steps executed with precise reasoning. Step 1's scarcity analysis (only three 6-halves, only two 5-halves) correctly predicted that Green 17 would consume high values, while the abundance of 0-halves and 1-halves filled Yellow Equal and Red Equal respectively. Every placement was mathematically inevitable given the constraints. Pips Hint: the final piece always validates your entire strategic plan—if it satisfies the last constraint perfectly, every scarcity-driven decision from Step 1 forward was logically sound and necessary.
🎥 Key Domino Placement Revealed | Pips NYT Puzzle Trick – November 29, 2025
Watch how one smart domino placement unlocks hidden constraints and reshapes the entire grid logic.
💡 Pro Tips for Similar Puzzles
Start with Constraints
Always begin with the most constrained regions - sum regions with small numbers or tight spaces.
Use Equal Regions
Use "equal" regions as anchors - they eliminate many possibilities quickly.
Work Systematically
Let the rules guide your placement rather than guessing randomly.
Double-Check
Verify each region's rules are satisfied before moving to the next.
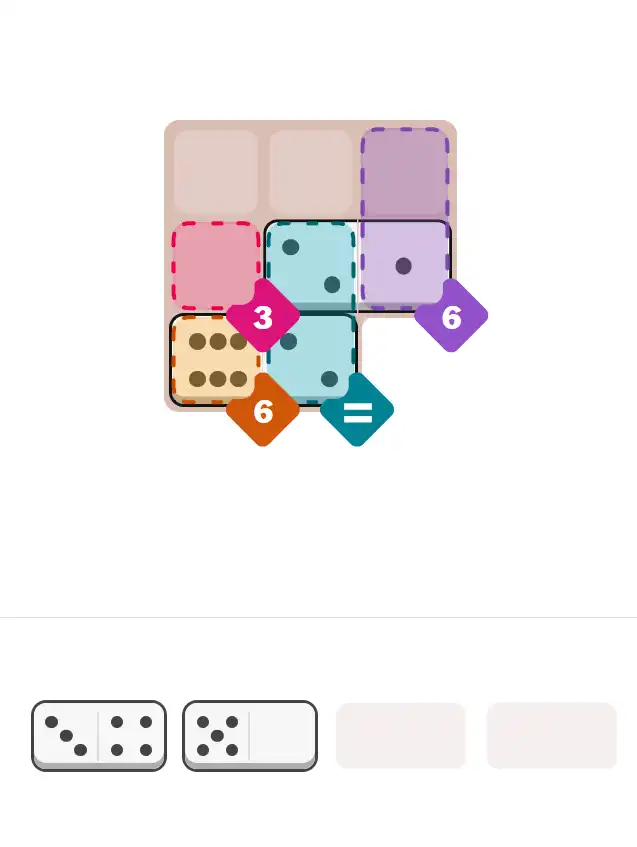
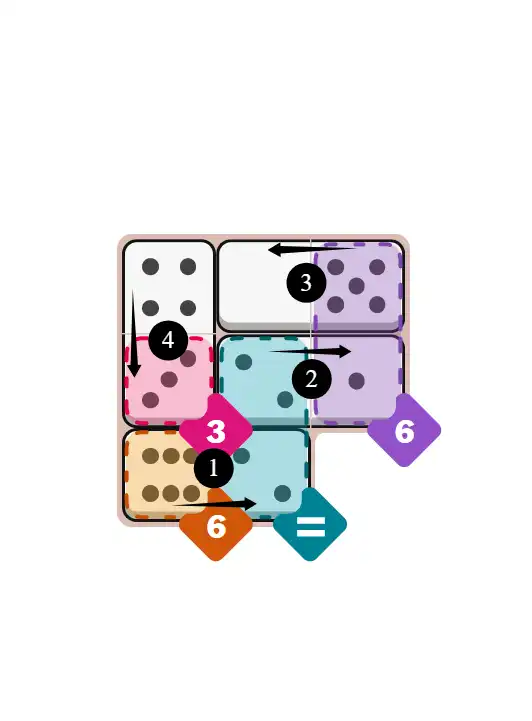
💬 Community Discussion
Leave your comment