🚨 SPOILER WARNING
This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!
Click here to play today's official NYT Pips game first.
Want hints instead? Scroll down for progressive clues that won't spoil the fun.
🎲 Today's Puzzle Overview
Start your Tuesday, November 26, 2025, with a trio of freshly crafted Pips NYT puzzles—each one shaped with deliberate structure and editorial clarity by Ian Livengood.
Today’s lineup brings a smooth difficulty curve: Easy #367 by Ian himself, followed by Medium #368 and Hard #369, both designed by the always-inventive Rodolfo Kurchan.
Across all three grids, you’ll find the kind of logical architecture puzzle solvers love discussing: compact sum-regions that reward early deductions, equals-clusters that tighten the solution space, and positional constraints that act like built-in Pips Hints guiding you toward the next forced placement.
Medium and Hard, in particular, showcase Rodolfo’s signature layering—subtle pip-economy pressure, narrow value windows, and region interlocks that create satisfying “click” moments when everything falls into place.
So grab your coffee, ping your favorite puzzle partner, and jump into the mix.
Whether you're comparing how you broke down those early constraint chains, sharing a Pips Hint that unlocked the grid, or posting your final solution path, November 26 delivers a full day of community-friendly logic exploration—and plenty of bragging rights for whoever solves the Hard grid first.
Written by July
Puzzle Analyst – Mark
💡 Progressive Hints
Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!
💡 Hint #1 - Observe
Dominoes Include: [5-2], [5-0], [4-3], [4-1], [4-0]. Only 3 domino halves that contain 4 pips.
💡 Hint #1 - Observe
Dominoes Include: [6-6], [6-3], [6-2], [5-1], [4-2], [3-2], [1-0]. Only 4 domino halves that contain 6 pips. [6-6] must placed in Purple Equal region. The domino halves in the Blue Number (11) region must be 5+6.
💡 Hint #1 - Observe
Dominoes Include: [6-5], [6-3], [5-4], [5-2], [5-1], [4-3], [3-3], [3-0], [2-2], [1-1]. Only 5 domino halves that contain 3 pips. [3-3] must placed in Yellow Equal region. Only 2 domino halves that contain 6 pips ([6-5], [6-3]).
💡 Hint #2 - Blue Number (15)
The domino halves in this region must be 5.
💡 Hint #3 - Purple Equal
The domino halves in this region must be 1.
💡 Hint #4 - Yellow Equal
The domino halves in this region must be 3.
💡 Hint #5 - Light Blue Equal
The domino halves in this region must be 4.
🎨 Pips Solver
Nov 26, 2025
Click a domino to place it on the board. You can also click the board, and the correct domino will appear.
✅ Final Answer & Complete Solution For Hard Level
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.
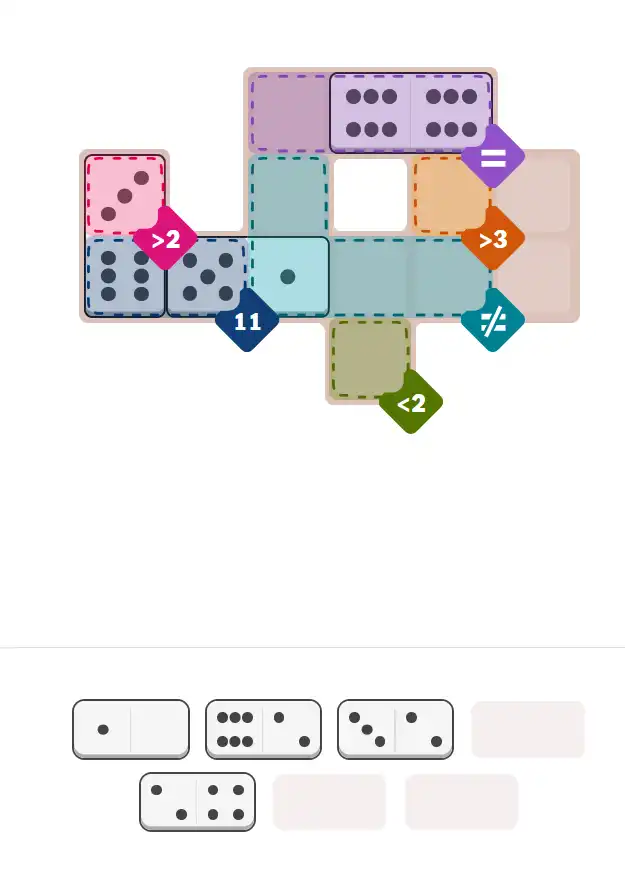
Starting Position & Key First Steps
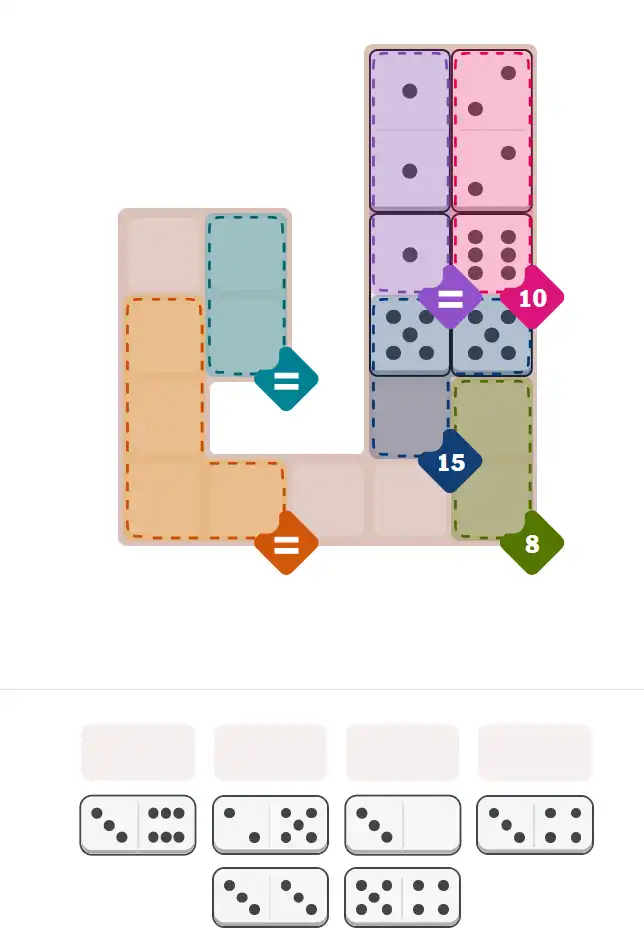
This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.
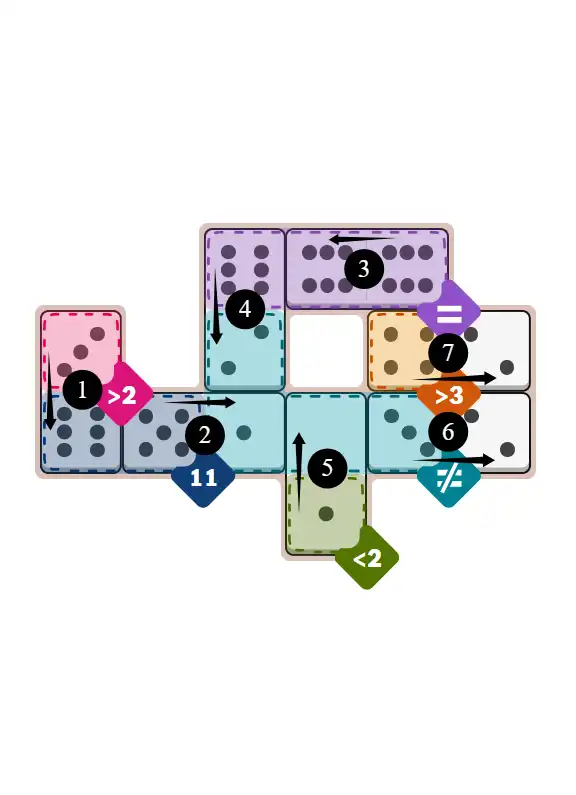
Final Answer: The Solved Grid for Hard Mode
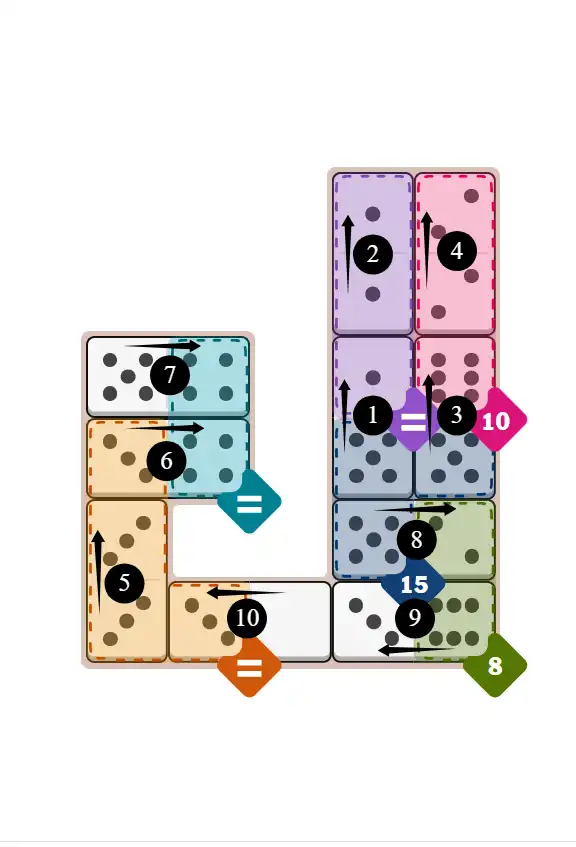
Compare this final grid with your own solution to see the correct placement of all dominoes.
🔧 Step-by-Step Answer Walkthrough For Easy Level
1
Step 1: Inventory and Equal Region Analysis
Dominoes: 5-2, 5-0, 4-3, 4-1, 4-0. Critical observation: only 3 domino halves contain 4-pips (from 4-3, 4-1, 4-0). Looking at the board, the Light Blue Equal region (center column) is the largest area and demands matching pip values throughout. With exactly three 4-halves available, this creates a perfect inventory match—the Light Blue Equal region MUST use all three 4-pips. For 5-pips: we have two 5-halves (from 5-2 and 5-0). The Red Equal region (top center-right) will need these 5s. This predetermined allocation drives our entire solution strategy. Pips Hint: when equal regions perfectly match your pip inventory counts, they become non-negotiable anchor points—identify these first before making any placements.
2
Step 2: Light Blue Equal Region - Strategic 4s Placement
From Step 1's analysis, this region needs all domino halves to show 4-pips. We have exactly three 4-halves available (from 4-3, 4-1, 4-0), matching the region's vertical cell count perfectly. Looking at the board layout and neighboring constraints, place the dominoes strategically: Place 4-3 horizontally (4-half in Light Blue Equal, 3 extends RIGHT into Yellow >2 region, satisfying 3>2 ✓). Place 4-1 horizontally (4-half in Light Blue Equal, 1 extends LEFT into Dark Blue >0 region, satisfying 1>0 ✓). Place 4-0 horizontally (4-half in Light Blue Equal, 0 extends LEFT into the blank area outside any constraint region). This placement not only fills the Light Blue Equal region with matching 4s but simultaneously satisfies two inequality constraints (>2 and >0) with the partner halves. Brilliant multi-constraint solving! Pips Hint: when placing dominoes in equal regions, choose orientations so partner halves satisfy adjacent inequality constraints—one smart placement can solve three problems at once.
3
Step 3: Red Equal Region - The 5s Complete the Puzzle
From Step 1, we identified two 5-halves (from 5-2 and 5-0) for the Red Equal region. This region demands matching pip values throughout. Place 5-0 horizontally (5-half in Red Equal, 0 extends LEFT into the Purple 0 region, satisfying that region's 0 requirement). Place 5-2 horizontally (5-half in Red Equal, 2 extends RIGHT into the blank area outside any constraint region). This completes both equal regions perfectly: Light Blue filled with three matching 4s, Red filled with two matching 5s. All neighboring constraints satisfied: Purple gets its 0, Yellow gets 3 (which is >2), Dark Blue gets 1 (which is >0). Puzzle complete through systematic equal-region prioritization and strategic orientation choices. Pips Hint: final equal regions validate your Step 1 inventory analysis—when all matching pips fit perfectly and all adjacent constraints align, your initial strategic planning was flawless.
🔧 Step-by-Step Answer Walkthrough For Medium Level
1
Step 1: Strategic Inventory - The 6-Pip Constraint
Dominoes: 6-6, 6-3, 6-2, 5-1, 4-2, 3-2, 1-0. Critical discovery: only 4 domino halves contain 6-pips (two from 6-6, one from 6-3, one from 6-2). Looking at the board, the Purple Equal region (top horizontal strip) is the largest equal constraint area, likely requiring multiple matching pips. With our limited 6-pip supply and the size of Purple Equal, the 6-6 domino MUST be placed there—it's the only domino providing two 6s in one piece, maximizing our scarce high-value allocation. Additionally, examining the Blue 11 region (center-left), we need high values to reach 11. Testing: 5+6=11 works perfectly, so Blue 11 needs one 5-pip and one 6-pip. Pips Hint: when high-value pips are scarce and multiple regions demand them, pre-allocate your biggest doubles to equal regions first—they lock in two matching halves efficiently.
2
Step 2: Red Greater-Than-2 + Blue Number 11 - Dual Solving
From Step 1, Blue 11 needs 5+6=11. We have 5-1 available for the 5, and we need a 6 from either 6-3 or 6-2. Looking at the board layout, the Red >2 region (top left) neighbors Blue 11. Testing which domino works: place 6-3 vertically with the 6-pip in Blue 11 and the 3-pip in Red >2 region (satisfying 3>2 ✓). Then place 5-1 horizontally with the 5-pip in Blue 11 and the 1-pip extending right. Blue calculation: 6+5=11 ✓. Red >2 receives 3 ✓. This strategic vertical placement of 6-3 serves both constraints simultaneously—the hallmark of efficient puzzle-solving. Pips Hint: when sum regions neighbor inequality regions, test which high-value dominoes can serve both—vertical vs horizontal orientation often determines which constraints you can satisfy together.
3
Step 3: Purple Equal Region - The 6s Complete the Pattern
From Step 1, we reserved 6-6 for this region. From Step 2, we used one 6 (from 6-3) in Blue 11. Remaining 6-pips: the other half of 6-6, plus 6-2. The Purple Equal region (top horizontal) demands all matching pips—it needs all 6s. Place 6-6 horizontally (both 6-halves in Purple Equal, filling two cells perfectly) and 6-2 vertically (6-half in Purple Equal, 2 extends downward into Light Blue Not-Equal region). Counting: three 6-halves now fill Purple Equal (two from 6-6, one from 6-2), completing this equal constraint. The 2 from 6-2 extending downward sets up Step 4's not-equal region. Pips Hint: when executing equal regions, place your double domino (like 6-6) first horizontally to claim two cells instantly, then add remaining matching halves from mixed dominoes to complete the pattern.
4
Step 4: Light Blue Not-Equal + Green Less-Than-2 + Yellow Greater-Than-3
Three constraints remain: Light Blue Not-Equal (≠), Green <2 (bottom center), and Yellow >3 (right side). From Step 3, we already have 2 (from 6-2) in Light Blue ≠. From Step 2, we have 1 (from 5-1) extending into Light Blue ≠. So Light Blue ≠ already contains 1 and 2. Remaining dominoes: 1-0, 3-2, 4-2. Here's the key analysis: Light Blue ≠ needs different values, so we need to add 0 and 3 to create diversity (avoiding duplicate 1s or 2s). Place 1-0 vertically with the 0-pip in Light Blue ≠ region (creating diversity: 0, 1, 2) and the 1-pip in Green <2 region (satisfying 1<2 ✓). Place 3-2 horizontally with the 3-pip in Light Blue ≠ region (adding another different value) and the 2-pip extending RIGHT into blank area. Place 4-2 horizontally with the 4-pip in Yellow >3 region (satisfying 4>3 ✓) and the 2-pip extending RIGHT into blank area. Light Blue ≠ now contains: 2, 1, 0, 3—all different values satisfying the not-equal constraint ✓. Green <2 gets 1 ✓. Yellow >3 gets 4 ✓. Puzzle complete! Pips Hint: not-equal regions require diversity, not specific values—when you already have some pips placed, add different values to maximize variety while using partner halves to satisfy adjacent inequality constraints.
🔧 Step-by-Step Answer Walkthrough For Hard Level
1
Step 1: Inventory Analysis - The 3-Pip and 6-Pip Constraints
Dominoes: 6-5, 6-3, 5-4, 5-2, 5-1, 4-3, 3-3, 3-0, 2-2, 1-1. Critical discoveries: only 5 domino halves contain 3-pips (two from 3-3, one each from 6-3, 4-3, 3-0). Looking at the Yellow Equal region (left side, vertical strip), it appears to need multiple matching pips. With 3-3 providing two 3s in one domino, it MUST be placed in Yellow Equal to efficiently claim that region. Additionally, only 2 domino halves contain 6-pips (from 6-5 and 6-3), making 6s extremely scarce. This scarcity will constrain our options significantly—we must plan carefully where each 6 goes. Pips Hint: when a pip value has very limited supply (like our 5 three-halves or 2 six-halves), identify which regions absolutely need them before making any placements—scarcity drives strategy.
2
Step 2: Blue 15 + Purple Equal + Red 10 - Triple Region Analysis
Three interconnected regions demand attention: Blue 15 (center-right), Purple Equal (top center), and Red 10 (top right). Let's analyze Blue 15 first—it needs exactly 15. Testing high-value combinations: 6+6+3=15 would work, but from Step 1, we only have TWO 6-halves total. If we used both 6s in Blue 15, we'd also need a 3, but checking our 3-pip inventory (only 5 total), that would leave insufficient 3s for Yellow Equal which needs multiple 3s. Therefore, Blue 15 cannot be 6+6+3. Alternative: 5+5+5=15 works! We have enough 5-halves. For Purple Equal, testing matching values: it must be 1s—we have 1-1 and 5-1, giving exactly two 1-halves. Place 5-1 vertically (5 in Blue 15, 1 in Purple Equal). Place 1-1 vertically (both 1s in Purple Equal). Place 6-5 vertically (5 in Blue 15, 6 in Red 10). Place 2-2 vertically (positioning for later steps). Blue 15 calculation: 5+5+5=15 ✓. Purple Equal gets matching 1s ✓. Red 10 receives the 6 as part of its sum ✓. Pips Hint: when multiple regions compete for scarce high-value pips, test combinations systematically—eliminate impossible allocations first, then verify the remaining option satisfies all constraints.
3
Step 3: Yellow Equal + Light Blue Equal - The 3s and 4s
From Step 1, we reserved 3-3 for Yellow Equal. Remaining dominoes with 3s and 4s: 6-3, 5-4, 4-3, 3-0. Yellow Equal (left vertical) needs all 3s. Light Blue Equal (top left area) needs matching pips—testing what's available, it must be 4s. We have 5-4 and 4-3 providing 4-halves. Place 3-3 vertically (both 3s in Yellow Equal). Place 4-3 horizontally (3 in Yellow Equal, 4 in Light Blue Equal). Place 5-4 horizontally (4 in Light Blue Equal, 5 extends elsewhere). Yellow now has three 3s (from 3-3 and 4-3). Light Blue has two matching 4s ✓. The strategic 4-3 placement serves both equal regions simultaneously. Pips Hint: when two equal regions compete for limited matching pips, use mixed dominoes (like 4-3) as bridges—one half satisfies one equal region, the other half satisfies the adjacent equal region.
4
Step 4: Green Number 8 - Strategic 2+6 Combination
This region (right side, vertical) needs exactly 8. Remaining dominoes: 6-3, 5-2, 3-0. Green 8 needs to sum to exactly 8. Testing: 2+6=8 works perfectly. We have 5-2 (with a 2-half) and 6-3 (with our last unused 6-half). Looking at the board layout carefully, place 5-2 horizontally (2 in Green 8, 5 extends into an appropriate area) and 6-3 horizontally (6 in Green 8, 3 extends LEFT into the blank area outside any constraint region). Green calculation: 2+6=8 ✓. Pips Hint: when sum regions need specific values, don't assume every pip must serve a constraint region—sometimes partner halves simply extend into blank space, and that's perfectly valid.
5
Step 5: Yellow Equal - The Final 3
Yellow Equal needs one more 3 to complete its matching pattern. Last domino remaining: 3-0. Place 3-0 horizontally with the 3-half in Yellow Equal region and the 0 extending downward into blank space or adjacent area. Yellow Equal now has all its 3s matched perfectly (from 3-3, 4-3, and 3-0) ✓. Checking the count: two 3s from 3-3, one from 4-3, one from 3-0 = four 3-halves total in Yellow Equal. Puzzle complete—all regions satisfied through systematic scarcity analysis and strategic placements. Pips Hint: the final domino confirms your entire solution strategy—if it fits perfectly and completes all remaining constraints, every decision from Step 1 onward was logically sound.
🎥 Catch a razor-sharp logic hint for today’s Pips NYT puzzle (November 26 2025)
Watch the moment one decisive domino placement unlocks the entire region flow.
💡 Pro Tips for Similar Puzzles
Start with Constraints
Always begin with the most constrained regions - sum regions with small numbers or tight spaces.
Use Equal Regions
Use "equal" regions as anchors - they eliminate many possibilities quickly.
Work Systematically
Let the rules guide your placement rather than guessing randomly.
Double-Check
Verify each region's rules are satisfied before moving to the next.
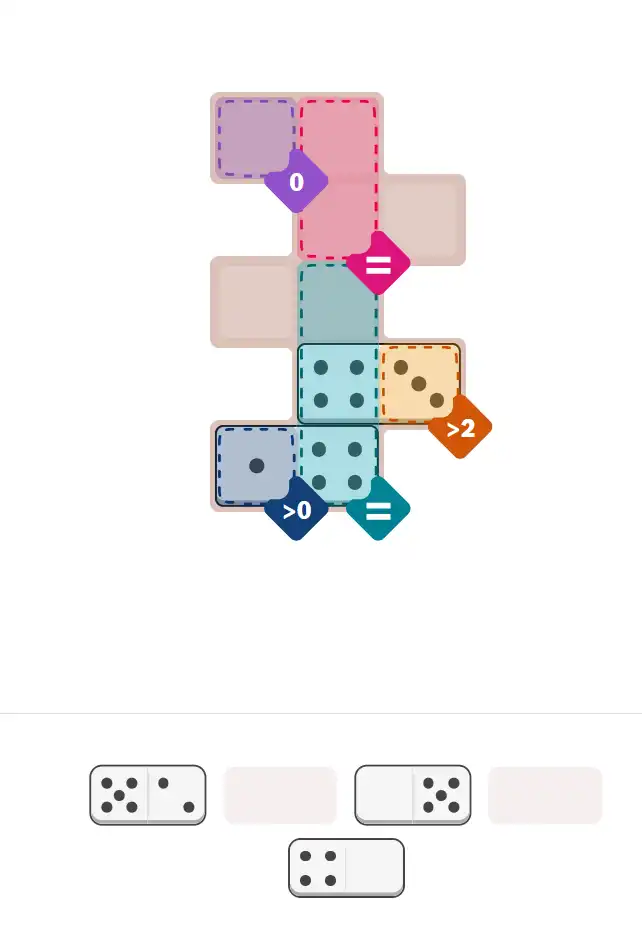
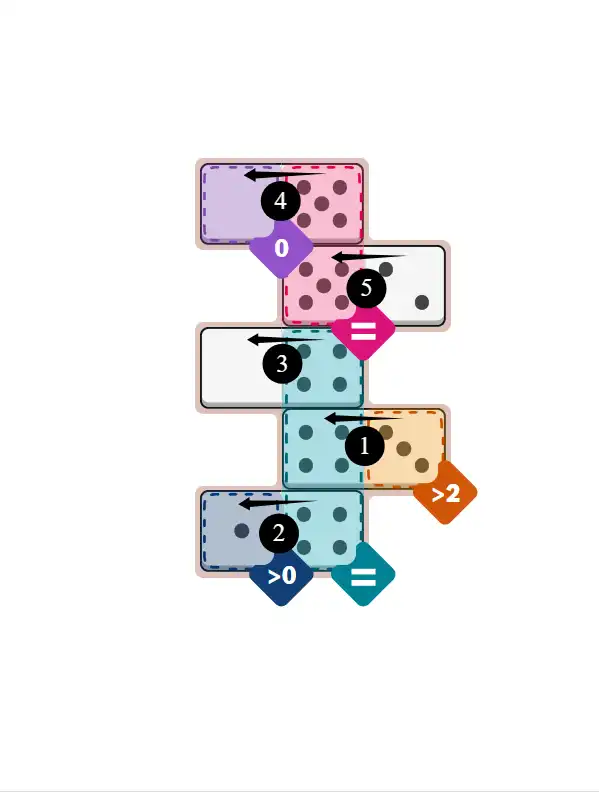
💬 Community Discussion
Leave your comment