NYT Pips Hint, Answer & Solution for January 8, 2026

Jan 8, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Thursday, January 8, 2026 opens the door to a fresh Daily Domino Puzzle, and it’s one that truly rewards slowing down and thinking out loud together.

As the new year settles in, today’s grid feels like an invitation to refocus, sharpen your logic, and enjoy that quiet satisfaction that comes from a well-placed domino.

Edited by Ian Livengood, this puzzle set is built for conversation.

It nudges players to pause, compare ideas, and swap a Pips Hint or two—because sometimes the best breakthrough comes from hearing how someone else reads the grid.

If you’re looking for a thoughtful pips hint today, this is a puzzle where small observations snowball into clean solutions.

The Easy puzzle (ID 497), constructed by Ian Livengood, works as a gentle warm-up.

Clear equals regions and modest sum targets help you build momentum, making it ideal for new solvers or for sharing quick hints within the community.

The Medium puzzle (ID 498), also by Ian Livengood, adds depth without feeling overwhelming.

Layered equals regions and tighter sums encourage discussion, careful counting, and that satisfying moment when the logic finally locks in.

For experienced players, the Hard puzzle (ID 499) by Rodolfo Kurchan is where collaboration really shines.

Unequal regions paired with precise sums demand patience, pattern recognition, and often a second opinion—perfect for group analysis or a full solution breakdown.

Whether you’re exchanging a quick pips hint, double-checking a solution, or proudly posting your completed grid, the January 8, 2026 Daily Domino Puzzle is all about community, thoughtful challenge, and shared discovery—one domino at a time.

Written by Anna

Puzzle Analyst – Mark

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - So easy

Can you?

💡 Hint #1 - Spot the unique pip early

Begin by identifying pip values that appear only once across all dominoes. A single-occurrence pip (like the lone 1) usually creates a forced placement and sets the direction for the entire puzzle.

💡 Hint #2 - Chain forced regions together

When a unique pip is placed, immediately follow the ripple effect across connected regions. Fixed targets such as exact sums, equals, and < constraints can often be resolved in one logical chain without branching.

💡 Hint #3 - Use equals regions to place doubles

After most singles are committed, equals regions naturally point to doubles. If one value is already present, the remaining equal region often collapses to a single domino, allowing the final placements to lock in cleanly.

💡 Hint #1 - Count scarce pips first

Start by scanning the full domino set and counting rare pip values. With only two halves showing 5 pips, those placements are immediately constrained, which forces Blue 9 to be 6+3 and narrows the Blue 5 region to just two candidate sums.

💡 Hint #2 - Lock forced zero placements

Regions with very small limits (<1) almost always force zeros. When only one domino contains a 0 pip, its orientation becomes fixed, giving you a guaranteed anchor early in the solve.

💡 Hint #3 - Resolve high-sum regions together

Pair connected high totals like Red 11 and Blue 9. By tracking which dominoes contain 6 pips, you can resolve both regions simultaneously instead of treating them separately.

💡 Hint #4 - Use unequal regions to fix doubles

Not-equal constraints are perfect for placing doubles. Once one value is already present, doubles like 4-4 or 5-5 often become the only legal way to satisfy adjacent equal or fixed-number regions.

💡 Hint #5 - Confirm sums by elimination

After major placements, re-check remaining dominoes. With 6s already used, Red 11 collapses to 6+5, Green 8 to 4+4, and Light Blue 4 to 2+2, turning multiple regions into forced moves.

💡 Hint #6 - Finish with leftover sums

In the final phase, look at what numbers are left rather than what you want. Remaining dominoes naturally fit Blue 5 and the last <4 constraint, letting the puzzle close cleanly without guessing.

🎨 Pips Solver

Jan 8, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

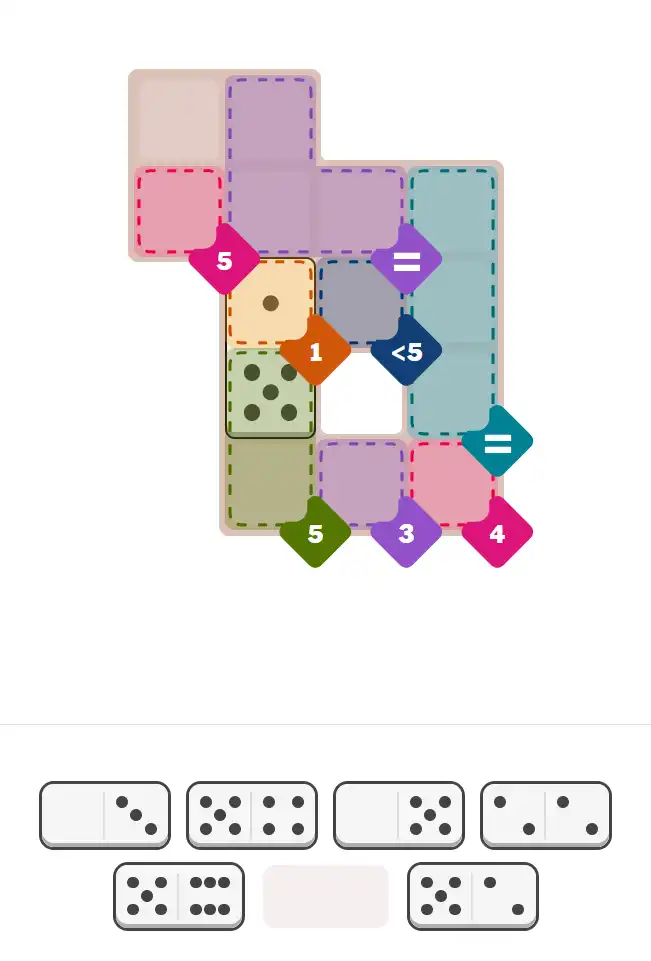
Starting Position & Key First Steps

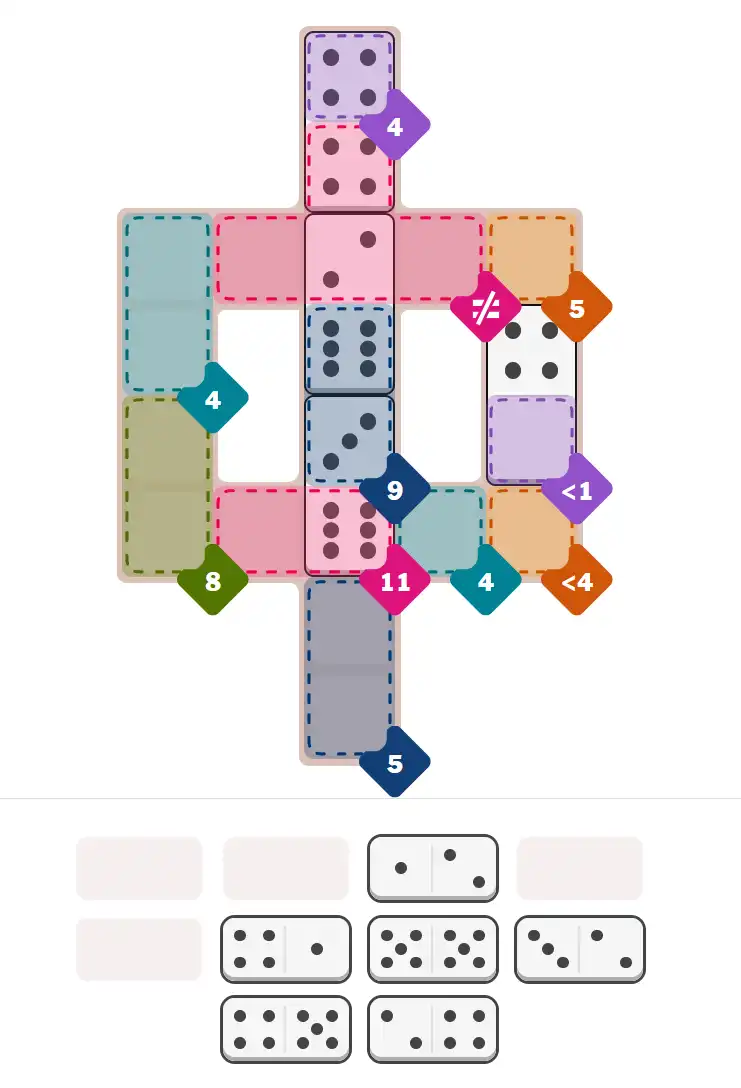
Pips hint for January 8, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

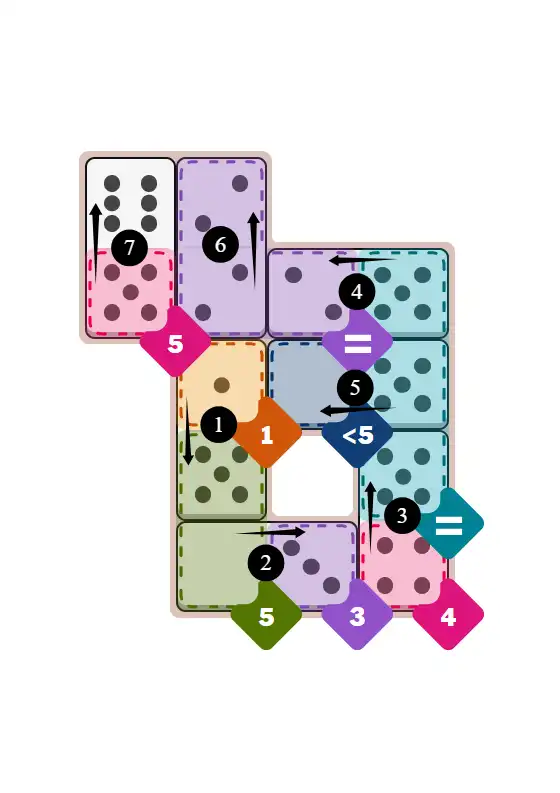
Final Answer: The Solved Grid for Hard Mode

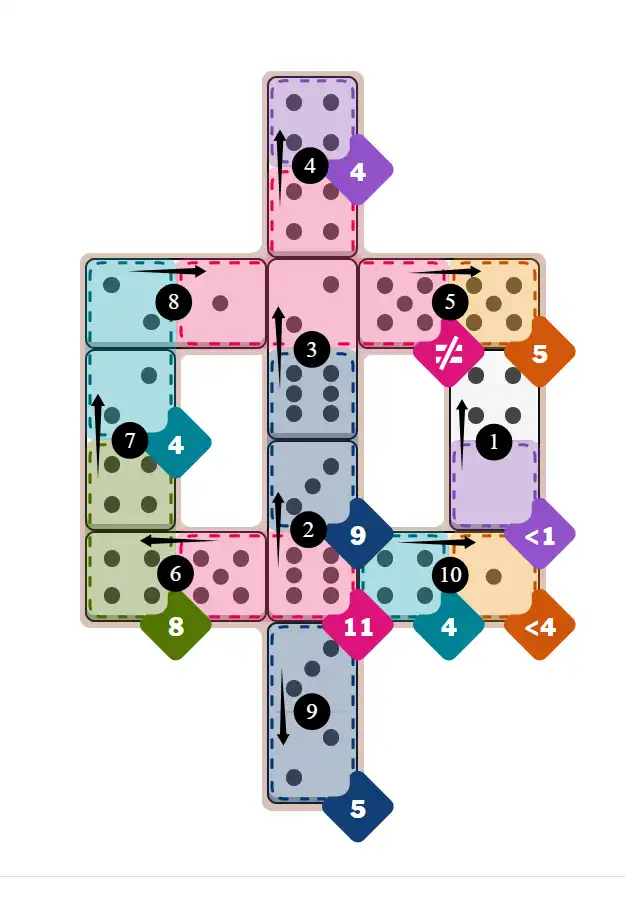
NYT Pips January 8, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-3], [6-2], [5-3], [3-0].

2

Step 2: Blue 6 + Red 8 + Purple Equal + Light Blue 6 + Yellow <3 --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Red 8 region must be 3+5. The domino halves in Purple Equal region must be 3. The domino halves in Light Blue 6 region must be 0+6. The answer is 6-3 (6 into Blue 6 region, 3 into Red 8 region), placed vertically; 5-3, placed horizontally; 3-0, placed vertically; 6-2 (6 into Light Blue 6 region, 2 into Yellow <3 region), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-5], [5-4], [5-2], [5-1], [5-0], [3-0], [2-2]. The single (unique) pips is the key to solving the Puzzle.

2

Step 2: Yellow 1 + Green 5 + Purple 3+ Red 4 + Light Blue Equal + Blue <5 --(Arrows ①②③④⑤)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 1 pips (5-1) and must placed vertically. The domino halves in Green 5 region must be 5+0. The domino halves in Light Blue Equal region must be 5. The answer is 1-5 (1 into Yellow 1 region), placed vertically; 0-3 (3 into Purple 3 region), placed horizontally; 4-5 (4 into Red 4 region), placed vertically; 5-2 (2 into Puple Equal region), placed horizontally; 5-0 (0 into Blue <5 region), placed horizontally.

3

Step 3: Purple Equal + Red 5 --(Arrows ⑥⑦)

Confirmed by neighboring region and step 2 and remaining dominoes (6-5, 2-2). The domino halves in Purple Equal region must be 2 (one 2s already come from step 2). The answer is 2-2, placed vertically; 5-6 (5 into Red 5 region, 6 up into blank), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-3], [6-2], [5-5], [5-4], [4-4], [4-2], [4-1], [4-0], [3-2], [2-1]. Only 2 domino halves that contain 5 pips, need one for Red 11 region, need one for Yellow 5 region. Therefore, the domino halves in Blue 9 region must be 6+3. Need one domino sum to be 5 (4-1 or 3-2) placed in Blue 5 region.

2

Step 2: Purple <1 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 0 pips (4-0). The answer is 0-4 (0 into Purple <1 region, 4 up into blank), placed vertically.

3

Step 3: Red 11 + Blue 9 --(Arrows ②③)

Confirmed by neighboring region and remaining dominoes. The domino halves in Red 11 region must be 5+6. The domino halves in Blue 9 region must be 6+3. Only 2 dominoes with 6 pips (6-3, 6-2). The answer is 6-3 (6 into Red 11 region), placed vertically; 6-2 (2 into Red Not Equal region), placed vertically.

4

Step 4: Red Not Equal + Purple 4 + Yellow 5 --(Arrows ④⑤)

Confirmed by all left regions and remaining dominoes (5-5, 5-4, 4-4, 4-2, 4-1, 3-2, 2-1). The domino halves in Red Not Equal region must be different (one 2s already come from step 3). [4-4] must placed in the boundary between Purple 4 region and Red Not Equal region. The answer is 4-4 (one 4s into Red Not Equal region, one 4s into Purple 4 region), placed vertically; 5-5 (one 5s into Red Not Equal region, one 5s into Yellow 5 region), placed horizontally.

5

Step 5: Red 11 + Green 8 + Left Light Blue 4 --(Arrows ⑥⑦⑧)

Confirmed by neighboring region and remaining dominoes (5-4, 4-2, 4-1, 3-2, 2-1). The domino halves in Red 11 region must be 6+5 (6s already come from step 3). The domino halves in Green 8 region must be 4+4. The domino halves in Left Light Blue 4 region must be 2+2. The answer is 5-4, placed horizontally; 4-2, placed vertically; 2-1 (1 into Red Not Equal region), placed horizontally.

6

Step 6: Blue 5 + Bottom Light Blue 4 + Yellow <4 --(Arrows ⑨⑩)

Confirmed by neighboring region and remaining dominoes (4-1, 3-2). The answer is 3-2 (sum to be 5 placed in Blue 5 region), placed vertically; 4-1 (4 into Bottom Light Blue 4 region, 1 into Yellow <4 region), placed horizontally.

🎥 NYT Pips Puzzle Solution | January 8, 2026 — Clean Logic, Smart Pips Hints, Full Breakdown

Solve smarter, not harder—and let the pips do the talking.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 9, 2026

View Answer →

NYT Pips Hints & Answers for January 7, 2026

View Answer →

NYT Pips Hints & Answers for January 6, 2026

View Answer →

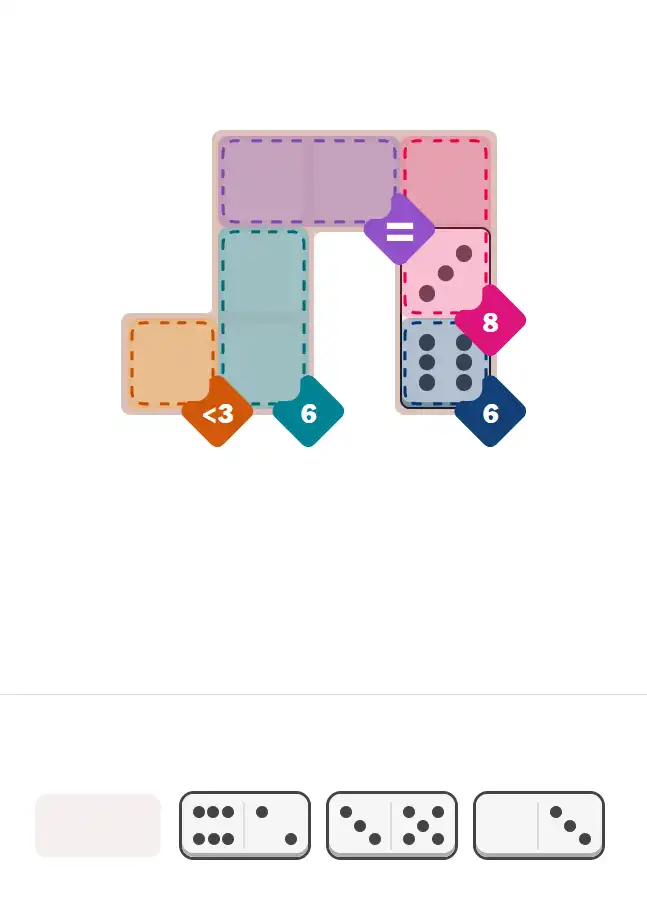
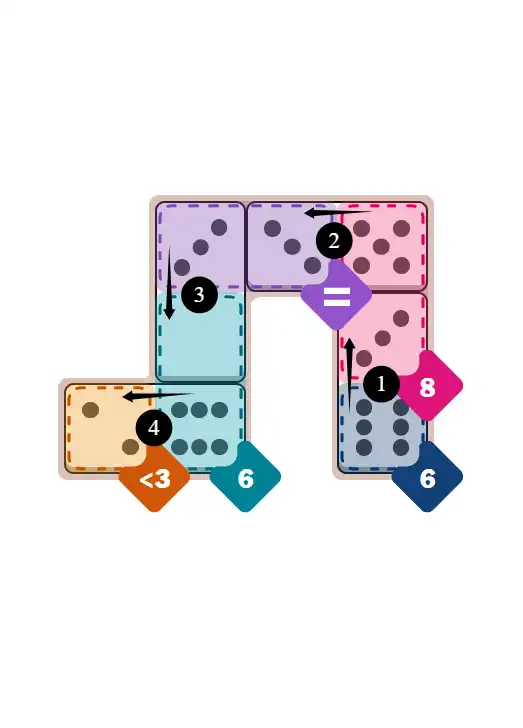
💬 Community Discussion

Leave your comment