NYT Pips Hint, Answer & Solution for January 9, 2026

Jan 9, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Friday, January 9, 2026 brings a fresh Daily Domino Puzzle that’s perfect for solvers who enjoy slowing down, thinking things through, and sharpening their logic.

As an early-January brain workout, it’s a great way to ease into the new year with a clean grid and a clear challenge—coffee optional, pips thinking required.

The Easy grid (ID 522) is an ideal warm-up.

With compact sums and straightforward equals regions, it helps you spot forced placements quickly and build confidence. This is where an early pips hint often makes everything click, setting the tone for the rest of the solve.

The Medium grid (ID 546) turns up the pressure.

Higher sum targets and multiple equals regions demand careful tracking of pips distribution, and casual guessing won’t get you far. A well-timed pips hint today—especially around shared regions—can save several moves and keep the logic flowing.

The Hard grid (ID 571), created by Rodolfo Kurchan, is a true logic workout.

Interconnected equals regions dominate the grid, rewarding disciplined analysis and clean deductions. This is the kind of puzzle where counting dominoes, revisiting assumptions, and refining your solution path pays off in a big way.

If you enjoy testing your logic, analyzing every domino, and improving how you use pips hints in real solves, the January 9, 2026 Daily Domino Puzzle delivers a deeply satisfying, data-driven challenge that’s worth every minute.

Written by Nikki

Puzzle Analyst – Sophia

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - So easy

Just do it

💡 Hint #1 - Count extreme sums first

When a region has a very high total like 17, break it into mandatory components. If only one domino can supply a critical pip (such as a single 6-6), that domino is immediately locked into the region, which also fixes how neighboring sum regions must be composed.

💡 Hint #2 - Place unique low pips early

Regions with strict upper bounds, such as less-than constraints, strongly favor the smallest available pip. If only one domino contains 0, its placement becomes forced and helps anchor the surrounding layout.

💡 Hint #3 - Resolve overlapping constraints together

When a sum region and an inequality region touch, solve them as a pair. Satisfying the exact total first often leaves only one valid way to meet the greater-than condition at the same time.

💡 Hint #4 - Reserve scarce values for required roles

If a future region still needs a specific pip value and only one domino can provide it, that domino cannot be spent elsewhere. This makes equal regions especially restrictive once rare pips are identified.

💡 Hint #5 - Finish by distributing remaining sums cleanly

After major regions are fixed, assign the leftover dominoes by matching exact totals and inequality rules simultaneously. At this stage, each placement typically satisfies multiple regions at once, closing the puzzle efficiently.

💡 Hint #1 - Start with frequency counting

When all regions are Equals and each needs four halves, begin by counting pip frequency. Numbers with limited identical dominoes (like doubles) reveal which values cannot fill equals regions and must be pushed into blank spaces.

💡 Hint #2 - Lock equals using shared boundaries

An Equals region touching multiple other Equals regions is highly constrained. If only one pip value can satisfy all shared boundaries without breaking other regions, that value is forced.

💡 Hint #3 - Preserve scarce high pips

High pips with few appearances (such as 6s) should be protected early. If an Equals region cannot absorb them cleanly, they are almost certainly destined for blank cells.

💡 Hint #4 - Use elimination across equals regions

Once one Equals region is fixed, eliminate its pip value from neighboring Equals regions. What remains is often a single viable pip that completes the region without conflict.

💡 Hint #5 - Assign remaining equals in pairs

With most constraints resolved, match the remaining Equals regions by pairing leftover dominoes whose pips appear in clean multiples. This final pass confirms both regions simultaneously and clears all blanks.

🎨 Pips Solver

Jan 9, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

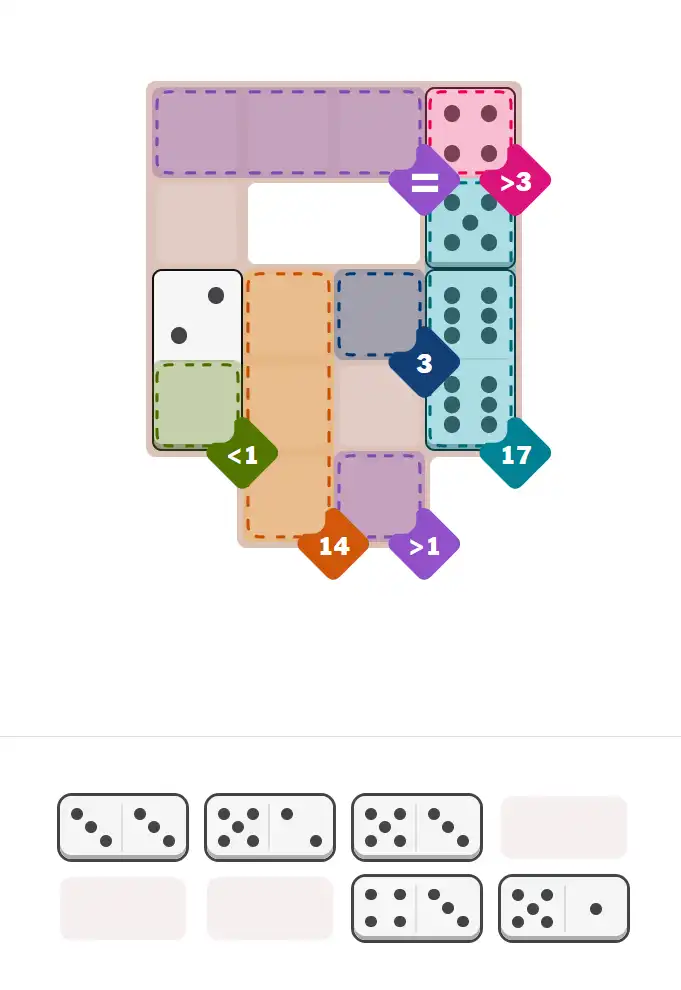
Starting Position & Key First Steps

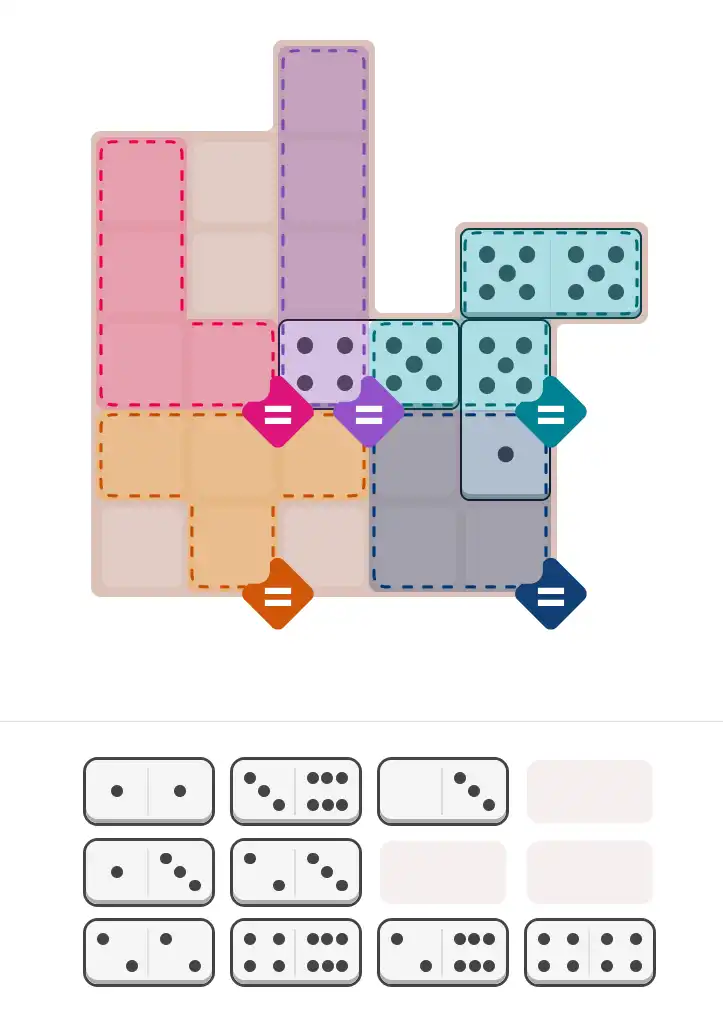
Pips hint for January 9, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

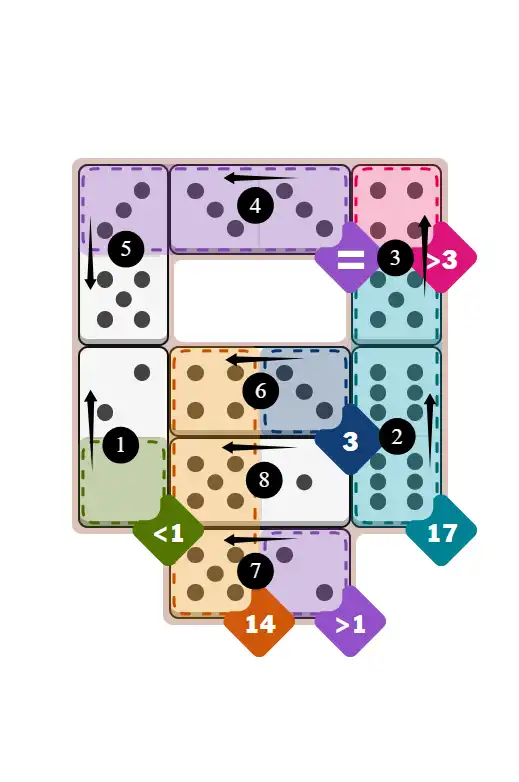
Final Answer: The Solved Grid for Hard Mode

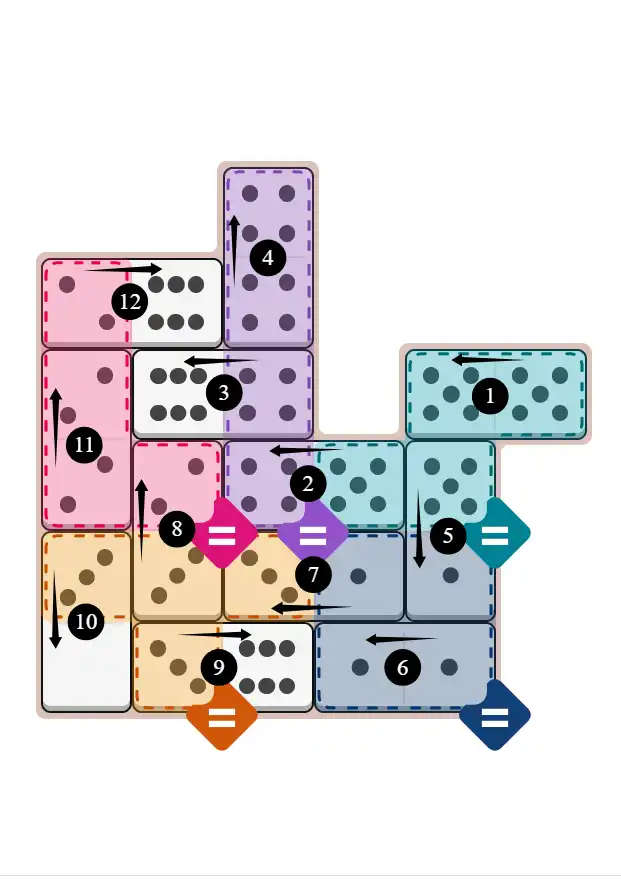
NYT Pips January 9, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-3], [6-1], [5-4], [3-3], [1-1].

2

Step 2: Purple 3 + Yellow >4 --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. Only the domino 6-3 can fit in these two regions. The answer is 3-6 (6 into Yellow >4 region), placed vertically.

3

Step 3: Red <2 + Light Blue 9 + Green 8 --(Arrows ②③④)

Confirmed by neighboring region and remaining dominoes (6-1, 5-4, 3-3, 1-1). The domino halves in Light Blue 9 region must be 6+3. The domino halves in Green 8 region must be 3+5. The answer is 1-6 (1 into Red <2 region), placed horizontally; 3-3, placed horizontally; 5-4 (4 right into blank), placed horizontally.

4

Step 4: Blue Equal --(Arrows ⑤)

The answer is 1-1, placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [5-4], [5-3], [5-2], [5-1], [4-3], [3-3], [2-0]. The domino halves in Light Blue 17 region must be 6+6+2, only one domino with 6 pips (6-6) for Light Blue 17 region. Therefore, the domino halves in Yellow 14 region must be 5+5+4.

2

Step 2: Green <1 --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 0 pips (2-0) and must placed vertically. The answer is 0-2 (0 into Green <1 region, 2 up into blank), placed vertically.

3

Step 3: Light Blue 17 + Red >3 --(Arrows ②③)

Confirmed by neighboring region and relative position and remaining dominoes. The domino halves in Light Blue 17 region must be 6+6+5. The answer is 6-6, placed vertically; 5-4 (4 into Red >3 region), placed vertically.

4

Step 4: Purple Equal --(Arrows ④⑤)

Confirmed by neighboring region and remaining dominoes (5-3, 5-2, 5-1, 4-3, 3-3). Need one domino with the same number placed in this region, only one domino left that contain 4 pips (4-3) for Yellow 14 region. The domino halves in Purple Equal region must be 3. The answer is 3-3, placed horizontally; 3-5 (5 down into blank), placed vertically.

5

Step 5: Yellow 14 + Blue 3 + Purple >1 --(Arrows ⑥⑦⑧)

Confirmed by neighboring region and remaining dominoes (5-2, 5-1, 4-3). The domino halves in Yellow 14 region must be 5+5+4. The answer is 3-4 (3 into Blue 3 region), placed horizontally; 2-5 (2 into Purple >1 region), placed horizontally; 1-5 (1 into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-4], [6-3], [6-2], [5-5], [5-4], [5-1], [4-4], [3-2], [3-1], [3-0], [2-2], [1-1]. All the regions are Equla regions and need 4 domino halves. Only 4 dominoes with the same number (5-5, 4-4, 2-2, 1-1), need one for Light Blue Equal, one for Purple Equal, and one for Blue Equal. Only 3 dominoes with 6 pips (6-4, 6-3, 6-2), 6 pips must place in blank.

2

Step 2: Light Blue Equal --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. The Light Blue Equal region is required to share a boundary with both the Purple Equal region and the Blue Equal region, only 3 dominoes with 5 pips (5-5, 5-4, 5-1), the domino containing 5 pips on one side has the other half with 1 pip and 4 pips. Therefore, the domino halves in Light Blue Equal region must be 5. The answer is 5-5, placed horizontally.

3

Step 3: Purple Equal --(Arrows ②③④)

Confirmed by neighboring region and step 2 and remaining dominoes. Only 3 dominoes with 4 pips (6-4, 5-4, 4-4), 6 pips must placed in blank. The domino halves in this region must be 4. The answer is 5-4 (5 into Light Blue Equal region), placed horizontally; 4-6 (6 left into blank), placed horizontally; 4-4, placed vertically.

4

Step 4: Blue Equal --(Arrows ⑤⑥⑦)

Confirmed by neighboring region and step 3 and remaining dominoes. The domino halves in this region must be 1. The answer is 5-1 (5 into Light Blue Equal region), placed vertically; 1-1, placed horizontally; 1-3 (3 into Yellow Equal region), placed horizontally.

5

Step 5: Yellow Equal + Red Equal --(Arrows ⑧⑨⑩⑪⑫)

Confirmed by neighboring region and step 4 and remaining dominoes (6-3, 6-2, 3-2, 3-0, 2-2). The domino halves in Yellow Equal region must be 3. The domino halves in Red Equal region must be 2. The answer is 3-2, placed vertically; 3-6 (6 right into blank), placed horizontally; 3-0 (0 down into blank), placed vertically; 2-2, placed vertically; 2-6 (6 right into blank), placed horizontally.

🎥 NYT Pips Domino Puzzle – January 9, 2026 | Full Easy–Hard Solve with Smart Pips Hints

Watch along, pause when needed, and let the logic unfold—one pip at a time

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 10, 2026

View Answer →

NYT Pips Hints & Answers for January 8, 2026

View Answer →

NYT Pips Hints & Answers for January 7, 2026

View Answer →

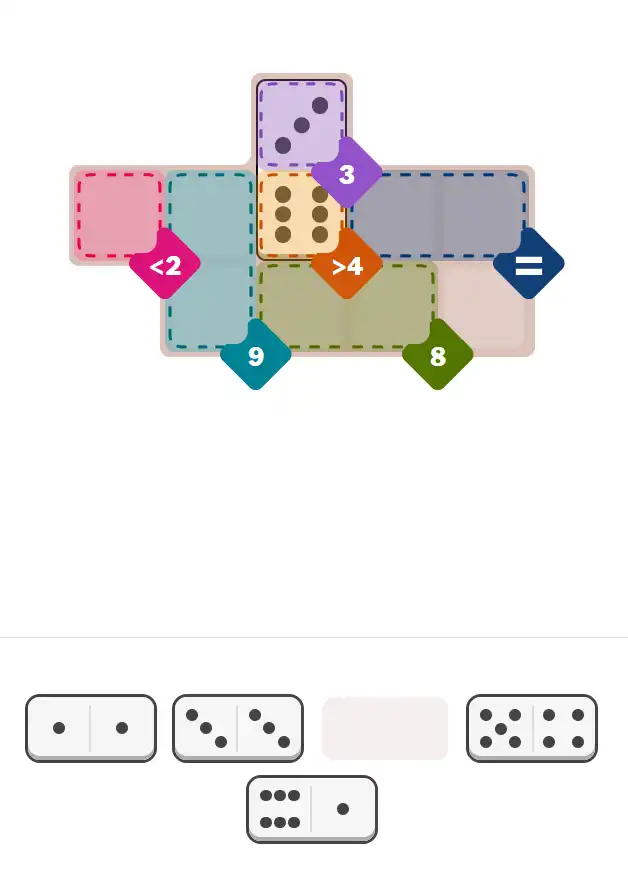
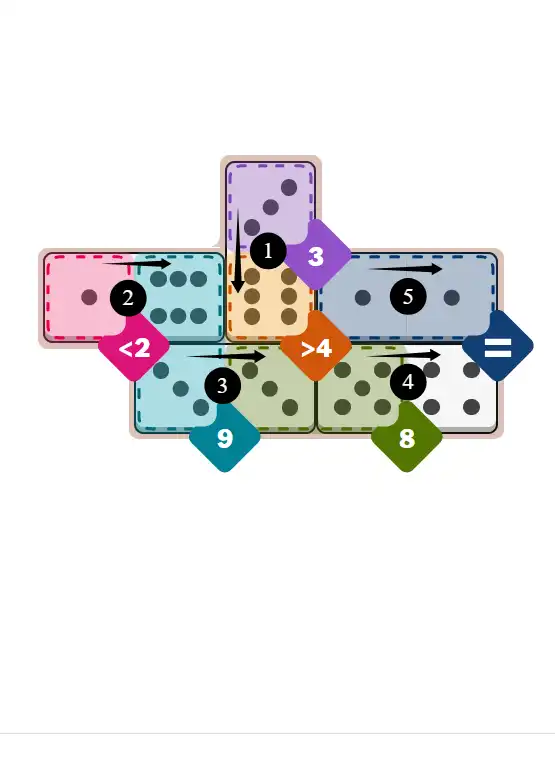
💬 Community Discussion

Leave your comment