NYT Pips Hint, Answer & Solution for January 10, 2026

Jan 10, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Saturday, January 10, 2026 opens the weekend with a Daily Domino puzzle that feels tailor-made for slow, thoughtful solving—and for talking it through together.

As a Saturday grid, it’s the perfect excuse to grab a coffee, sit back, and enjoy a more relaxed pace of play.

Edited by Ian Livengood, today’s puzzles encourage players to pause between moves, compare ideas, and share that satisfying moment when a stubborn region finally clicks. This is the kind of board where a single pips hint today can unlock several follow-up placements, rewarding careful observation rather than rushing.

The Easy puzzle (ID 513), constructed by Ian Livengood, offers a friendly entry point. Clear equals regions and modest sum targets guide early placements, making it ideal for warming up and trading first impressions or starter hints with friends.

Stepping up, the Medium puzzle (ID 539) by Rodolfo Kurchan introduces greater-than constraints paired with balanced sums. Here, counting dominoes and tracking remaining pips becomes essential, and shared logic often leads to faster breakthroughs.

For those craving a deeper challenge, the Hard puzzle (ID 560)—also by Rodolfo Kurchan—unfolds into a dense network of inequalities. This grid truly shines when solved collaboratively, with step-by-step solution analysis and careful breakdowns of forced moves.

Whether you’re posting a quick pips hint, checking a full solution, or solving side by side over the weekend, the January 10, 2026 Daily Domino puzzle is all about community, challenge, and the quiet joy of discovering the logic hidden in the grid.

Written by Bosco

Puzzle Analyst – Lucas

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - Observe

The single (unique) pips is the key to solving the Puzzle.

💡 Hint #1 - Identify mandatory sum regions first

Start by scanning for regions that demand an exact total, such as a fixed sum of 7 or a strict greater-than rule. These conditions immediately narrow the list of usable dominoes and define early priorities.

💡 Hint #2 - Let equals regions decide the doubles

Equals regions are powerful filters. When only a few doubles are available, determine which values can safely repeat without blocking nearby sum or inequality regions.

💡 Hint #3 - Solve exact sums before inequalities

Regions with exact targets, like a sum of 7, usually have very limited options. Locking these in early reduces uncertainty before tackling flexible greater-than regions.

💡 Hint #4 - Reserve large pips for high-threshold regions

When a region requires a total greater than a high number, save the largest remaining pips for it. This avoids wasting big values in low-impact areas.

💡 Hint #5 - Use leftovers to complete flexible regions

Once fixed sums and high thresholds are resolved, remaining dominoes typically fit only one place. Use elimination to drop them into open or loosely constrained regions to finish cleanly.

💡 Hint #1 - Count rare pips before placing anything

Start by counting how many times each pip value appears across all dominoes. Scarce numbers like 2s and 1s immediately constrain multiple regions and define which sums or equals regions are forced early.

💡 Hint #2 - Lock high-sum regions with obvious totals

Regions requiring large totals, such as a sum of 11, often have only one viable domino. Resolving these early removes high-value pips from circulation and simplifies later inequalities.

💡 Hint #3 - Resolve fixed totals by splitting pip budgets

When several regions demand exact low totals (like 2 or 1), distribute the available pips carefully. Once those budgets are exhausted, the remaining pips naturally funnel into higher-threshold regions.

💡 Hint #4 - Use last-remaining pips to force placements

When only one domino containing a specific pip remains, its placement becomes unavoidable. Use this moment to satisfy multiple regions at once and reduce branching.

💡 Hint #5 - Equals regions favor doubles late

As options narrow, equals regions often collapse to doubles. When other values are blocked by neighboring constraints, placing a double can stabilize several regions simultaneously.

💡 Hint #6 - Greater-than regions consume large values

Inequality regions with high thresholds naturally absorb the largest remaining dominoes. Assign these first to avoid accidentally trapping large pips in low-cap regions.

💡 Hint #7 - Pair leftover high pips deliberately

When a region already contains a large pip, look for the smallest partner that still satisfies the condition. This preserves flexibility elsewhere on the grid.

💡 Hint #8 - Use inequality cleanup to place leftovers

Once most sums are fixed, greater-than and less-than regions become simple filters. Match the remaining dominoes by eliminating any option that violates the inequality.

💡 Hint #9 - Balance high and low caps together

Solve paired constraints by considering both sides at once: high-threshold regions need big totals, while low-cap regions reject them. This dual reasoning quickly isolates valid placements.

💡 Hint #10 - Finish with forced low-sum placements

At the endgame, low-cap regions usually accept only one possible domino. Use these to place the final non-double pieces cleanly.

💡 Hint #11 - Close with the only remaining double

When all constraints are satisfied except one bounded region, the last unused double typically fits by elimination, completing the grid without ambiguity.

🎨 Pips Solver

Jan 10, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

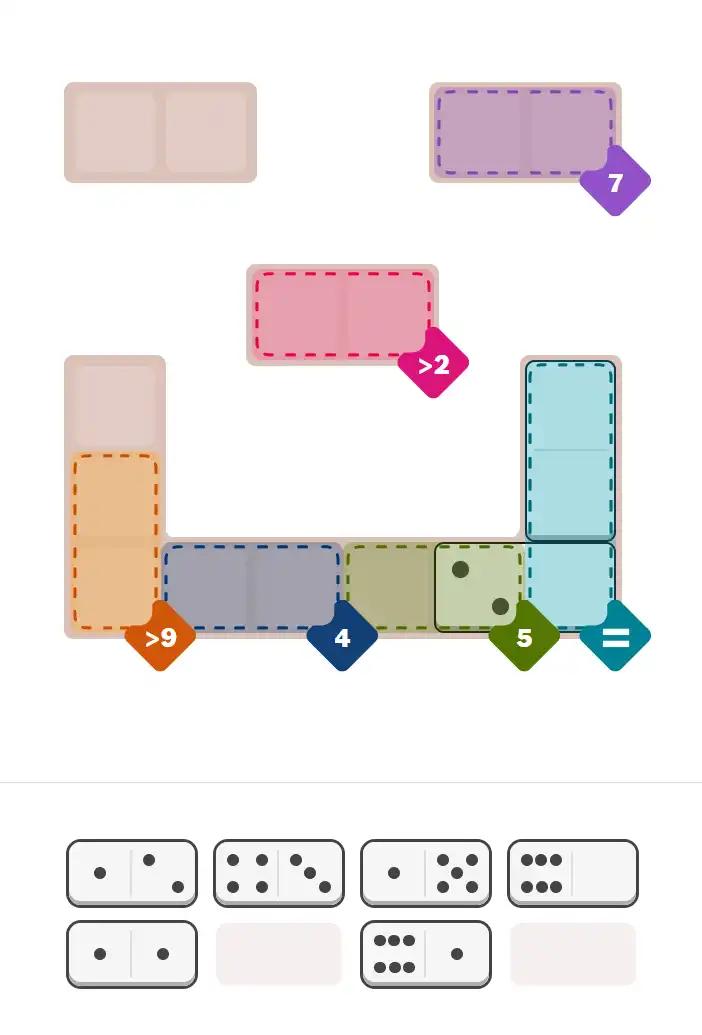
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

Starting Position & Key First Steps

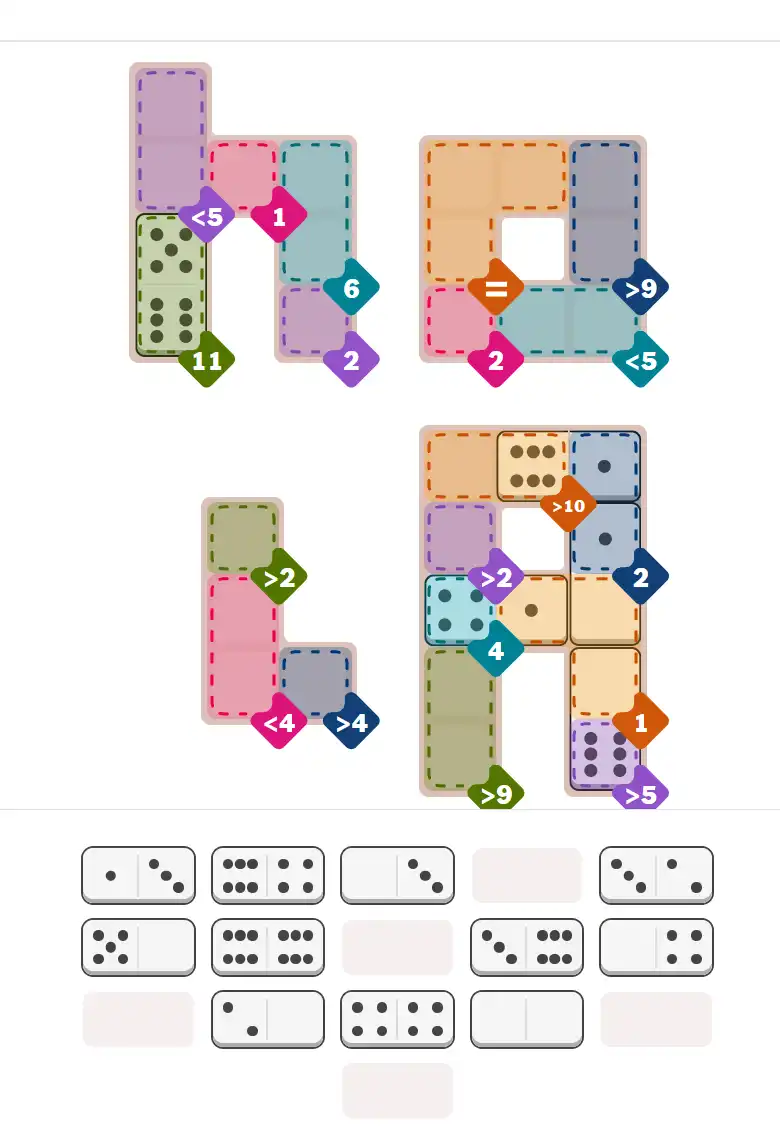
Pips hint for January 10, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

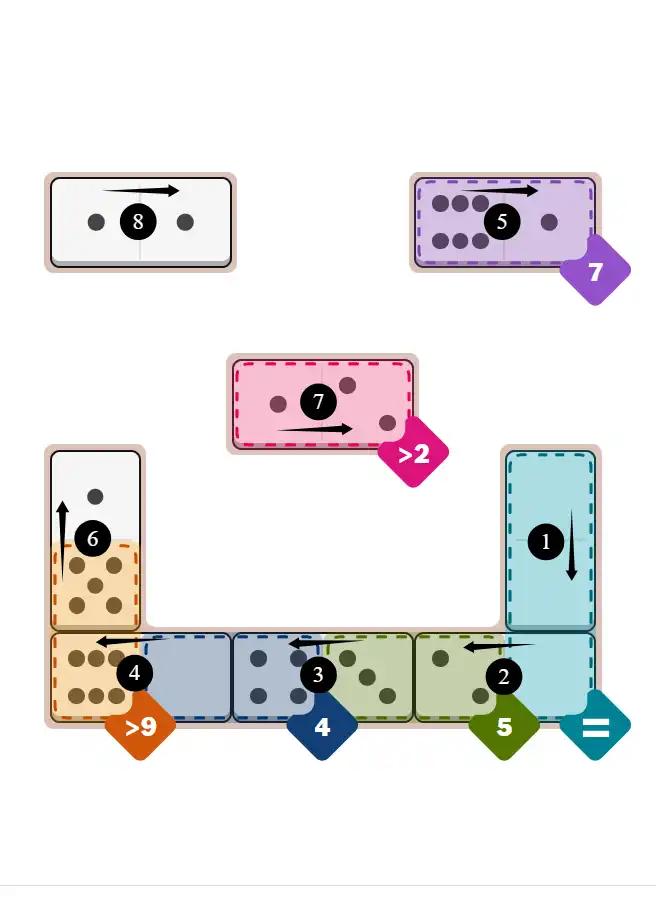
Final Answer: The Solved Grid for Hard Mode

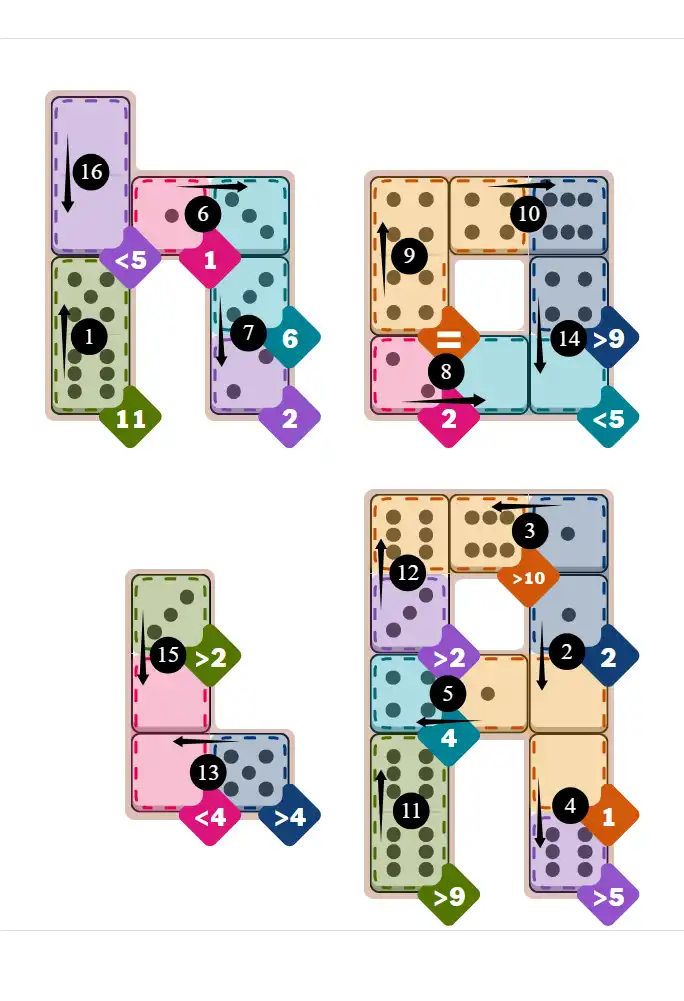
NYT Pips January 10, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-2], [6-1], [5-1], [4-0], [3-0], [1-1]. The single (unique) pips is the key to solving the Puzzle.

2

Step 2: Green 3 + Purple Equal + Blue 9 + Light Blue Equal --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. Only one domino with the 3 pips (3-0). The domino halves in Purple Equal region must be 0. The domino halves in Blue 9 region must be 4+5. The domino halves in Light Blue Equal region must be 1. The answer is 3-0 (3 into Green 3 region), placed horizontally; 0-4, placed horizontally; 5-1, placed vertically; 1-1, placed horizontally.

3

Step 3: Red >1 + Purple 6 + Yellow 1 --(Arrows ⑤⑥)

Confirmed by neighboring region and remaining dominoes (6-2, 6-1). The answer is 2-6 (2 into Red >1 region, 6 into Purple 6 region), placed horizontally; 1-6 (1 into Yellow 1 region, 6 right into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-1], [6-0], [5-1], [4-3], [2-1], [2-0], [1-1], [0-0]. Need one domino sum to be 7 placed in Purple 7 region. Need one domino sum to be more than 2 placed in Red >2 region.

2

Step 2: Light Blue Equal + Green 5 + Blue 4 --(Arrows ①②③④)

Need one domino with the same number (1-1 or 0-0) placed in Light Blue Equal region. Confirmed by all regions and step 1 and relative position. The domino halves in Light Blue Equal region must be 0. The domino halves in Green 5 region must be 2+3. The domino halves in Blue 4 region must be 4+0. The answer is 0-0, placed vertically; 0-2, placed horizontally; 3-4, placed horizontally; 0-6 (6 into Yellow >9 region), placed horizontally.

3

Step 3: Purple 7 --(Arrows ⑤)

Confirmed by neighboring region and remaining dominoes (6-1, 5-1, 2-1, 1-1). Need one domino sum to be 7 placed in this region. The answer is 6-1, placed horizontally.

4

Step 4: Yellow >9 --(Arrows ⑥)

Confirmed by neighboring region and remaining dominoes (5-1, 2-1, 1-1). The domino halves in this region must be 6+5 (6s already come from step 2). The answer is 5-1 (1 up into blank), placed vertically.

5

Step 5: Red >2 +Left Top Blank --(Arrows ⑦⑧)

Confirmed by neighboring region and remaining dominoes (2-1, 1-1). The answer is 1-2 (whole domino into Red >2 region), placed horizontally; 1-1 (whole domino into Left Top Blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-6], [6-5], [6-4], [6-3], [6-1], [6-0], [5-0], [4-4], [4-1], [4-0], [3-2], [3-1], [3-0], [2-0], [1-0], [0-0]. Only 2 dominoes with 2 pips (3-2, 2-0) for Purple 2 region and Red 2 region. Therefore, the domino halves in Blue 2 region must be 1+1 and come from two different dominoes. The the domino halves in Yellow 1 region must be 0+0+1. Only 4 domino halves that contain 1 pips (6-1, 4-1, 3-1, 1-0), need two for Blue 2 region, need one for Yellow 1 region, need one for Red 1 region.

2

Step 2: Green 11 --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. Need one domino sum to be 11 placed in this region. The answer is 6-5, placed vertically.

3

Step 3: Blue 2 + Yellow 1 + Purple >5 + Light Blue 4 --(Arrows ②③④⑤)

Confirmed by neighboring region and step 1 and remaining dominoes. The domino halves in Blue 2 region must be 1+1. The domino halves in Yellow 1 region must be 0+0+1. The answer is 1-0, placed vertically; 1-6 (6 into Yellow >10 region), placed horizontally; 6-0 (6 into Purple >5 region), placed vertically; 1-4 (1 into Yellow 1 region, 4 into Light Blue 4 region), placed horizontally.

4

Step 4: Red 1 + Light Blue 6 + Purple 2 --(Arrows ⑥⑦)

Confirmed by neighboring region and remaining dominoes. Only one domino left that contain 1 pips (3-1). The domino halves in Light Blue 6 region must be 3+3. The answer is 1-3 (1 into Red 1 region), placed horizontally; 3-2 (2 into Purple 2 region), placed vertically.

5

Step 5: Red 2 + Yellow Equal --(Arrows ⑧⑨⑩)

Confirmed by all left regions and remaining dominoes (6-6, 6-4, 6-3, 5-0, 4-4, 4-0, 3-0, 2-0, 0-0). Need one domino with the same number placed in Yellow Equal region. The domino halves in Yellow Equal region must be 4. The answer is 2-0 (2 into Red 2 region, 0 into Light Blue <5 region), placed horizontally; 4-4, placed vertically; 4-6 (6 into Blue >9 region), placed horizontally.

6

Step 6: Green >9 --(Arrows ⑪)

Confirmed by neighboring region and remaining dominoes (6-6, 6-3, 5-0, 4-0, 3-0, 0-0). Need one domino sum to be more than 9 placed in this region. The answer is 6-6 (whole domino), placed vertically.

7

Step 7: Purple >2 + Yellow >10 --(Arrows ⑫)

Confirmed by neighboring region and remaining dominoes (6-3, 5-0, 4-0, 3-0, 0-0). The domino halves in Yellow 10 region must add up to be more than 10 (one 6s already come from step 3). The answer is 3-6 (3 into Purple >2 region, 6 into Yellow >10 region), placed vertically.

8

Step 8: Blue >4 --(Arrows ⑬)

Confirmed by neighboring region and remaining dominoes (5-0, 4-0, 3-0, 0-0). The answer is 5-0 (5 into Blue >4 region, 0 into Red <4 region), placed horizontally.

9

Step 9: Blue >9 + Light Blue <5 --(Arrows ⑭)

Confirmed by neighboring region and remaining dominoes (4-0, 3-0, 0-0). The domino halves in Blue >9 region must add up to be more than 9 (6s already come from step 5). The domino halves in Light Blue <5 region must add up to be less than 5 (0s already come from step 5). The answer is 4-0 (4 into Blue >9 region, 0 into Light Blue <5 region), placed vertically.

10

Step 10: Green >2 + Red <4 --(Arrows ⑮)

Confirmed by neighboring region and remaining dominoes (3-0, 0-0). The domino halves in Red <4 region must add up to be less than 4 (0s already come from step 8). The answer is 3-0 (3 into Green >2 region, 0 into Red <4 region), placed vertically.

11

Step 11: Purple <5 --(Arrows ⑯)

The answer is 0-0 (whole domino into this region), placed vertically.

🎥 NYT Pips Solution Breakdown – January 10, 2026 | Easy to Hard Domino Logic Explained

Help you understand why each move works—not just what goes where.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 9, 2026

View Answer →

NYT Pips Hints & Answers for January 8, 2026

View Answer →

NYT Pips Hints & Answers for January 7, 2026

View Answer →

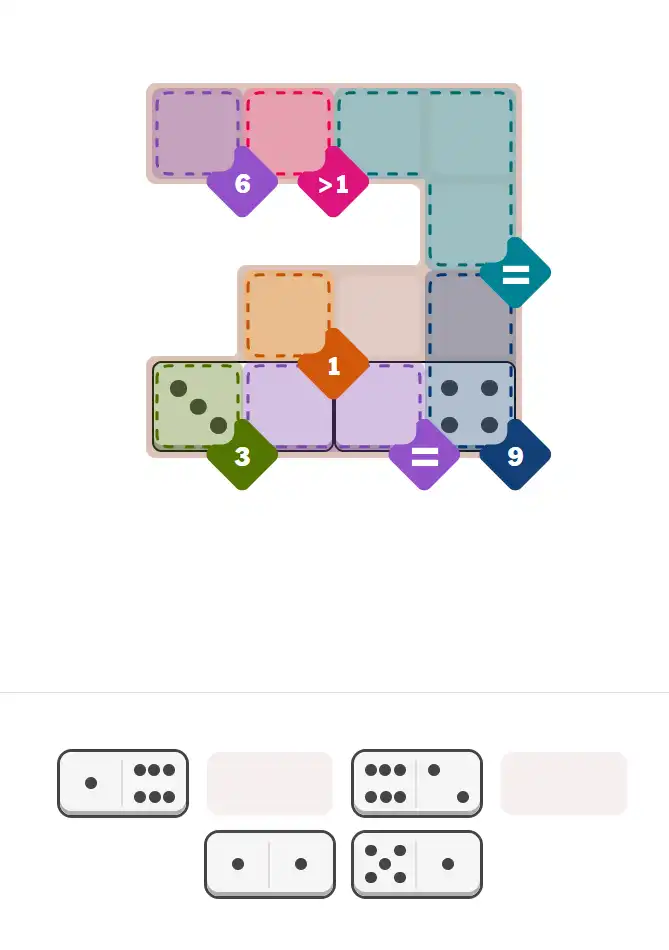
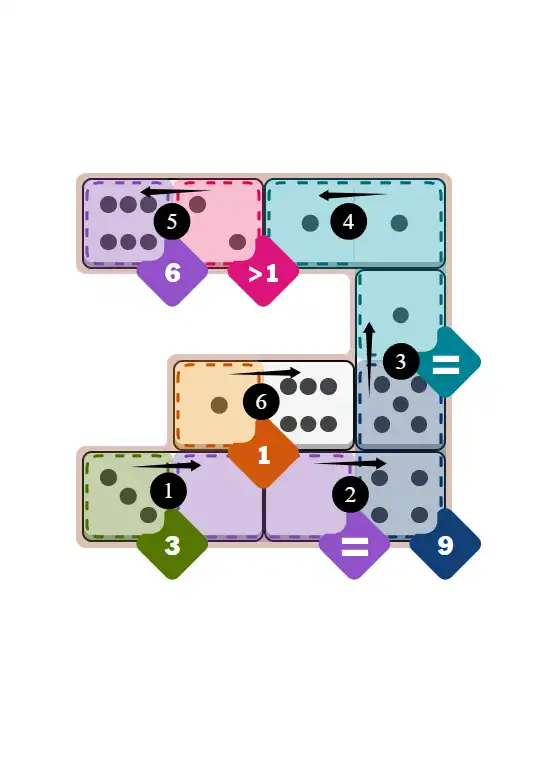
💬 Community Discussion

Leave your comment