NYT Pips Hint, Answer & Solution for January 7, 2026

Jan 7, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Wednesday, January 7, 2026 brings another Daily Domino Puzzle that feels especially suited for shared solving and thoughtful discussion.

With the New Year rhythm settling in, today’s grid invites solvers to slow down, compare ideas, and enjoy the calm focus that comes from steady, logical progress.

Edited by Ian Livengood, this puzzle set emphasizes clarity over speed. It’s a great day to exchange a pips hint today, talk through region logic, and appreciate how small insights unlock larger sections of the board.

The Easy puzzle (ID 479), constructed by Ian Livengood, works as a smooth entry point. Balanced sum regions and clean equals logic make it ideal for warming up, explaining techniques, or sharing quick Pips Hints with newer players.

Moving up, the Medium puzzle (ID 481) by Rodolfo Kurchan adds depth through tighter equals relationships, rewarding careful placement and step-by-step analysis.

For collaborative deep thinkers, the Hard puzzle (ID 487)—also by Rodolfo Kurchan—offers a layered grid where strategy discussion, constraint tracking, and full solution breakdowns truly shine.

Whether you’re posting a single hint, checking a complete solution, or solving side by side with friends, the January 7, 2026 Daily Domino Puzzle is built around community, logic, and that satisfying moment when every domino finally clicks into place.

Written by July

Puzzle Analyst – Nikki

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - A piece of cake

Enjoy it

💡 Hint #1 - Count Minimums and Locked Zeros

Begin by checking the smallest possible sums and pips. If a region requires a value below the minimum achievable by any non-zero domino, zeros are forced. Use this to immediately reserve 0–0 style placements and narrow equal regions to only the highest remaining pips.

💡 Hint #2 - Vertical Forcing with Scarce Pips

When only a few dominoes contain a critical pip (like 0), their orientation often becomes forced. Place these dominoes first, then let Equal regions and exact-sum regions cascade into fixed values through elimination.

💡 Hint #3 - Finish with Inequality Pairing

Once most values are known, inequality regions (> or <) usually collapse to a single valid pairing. Match remaining dominoes by checking which pip satisfies both the inequality and neighboring confirmed regions.

💡 Hint #1 - Pips Inventory Control

Start by counting rare pips. Zero-pip halves are limited, so immediately reserve them for regions that explicitly require 0 or very small totals. This prevents later conflicts and narrows valid placements early.

💡 Hint #2 - Force High Pips First

Inequality regions (>5, >8) are powerful filters. Lock in the highest available pips first, then check which remaining domino halves can still satisfy neighboring equal regions. Use overlap between constraints to force placements.

💡 Hint #3 - Eliminate Impossible Sums

When no domino can make certain sums (like 1 or 9), flip the logic: deduce exact pairs that must fill those regions. Combine pip scarcity (0s and 1s) with sum targets to resolve multiple regions at once.

💡 Hint #4 - Reuse Confirmed Logic

Return to earlier deductions. Once a value is fixed in an Equal region, re-check adjacent inequality regions. Previously ambiguous dominoes often become forced after one side is confirmed.

💡 Hint #5 - Match Pairs with Constraints

Use exact-sum regions to lock specific pairs, then apply Not Equal rules to separate remaining values. Look for regions where only one pairing satisfies both sum and comparison rules.

💡 Hint #6 - Clean Up with Singles

At the end, unresolved regions usually accept only one remaining domino. Scan for leftovers that trivially satisfy the final inequality or bound—these are safe, automatic placements.

🎨 Pips Solver

Jan 7, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

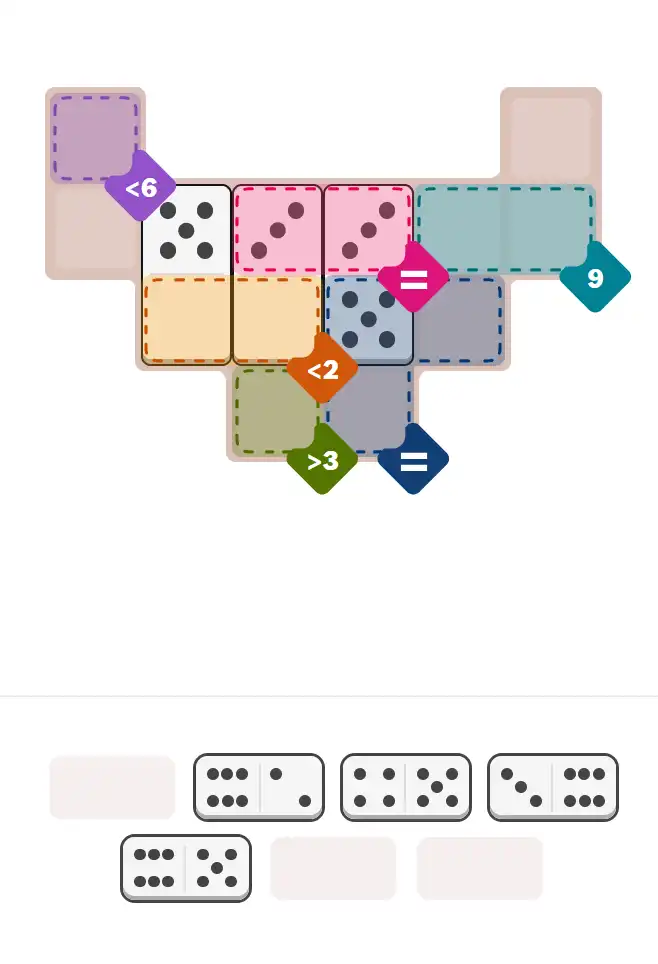
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

Starting Position & Key First Steps

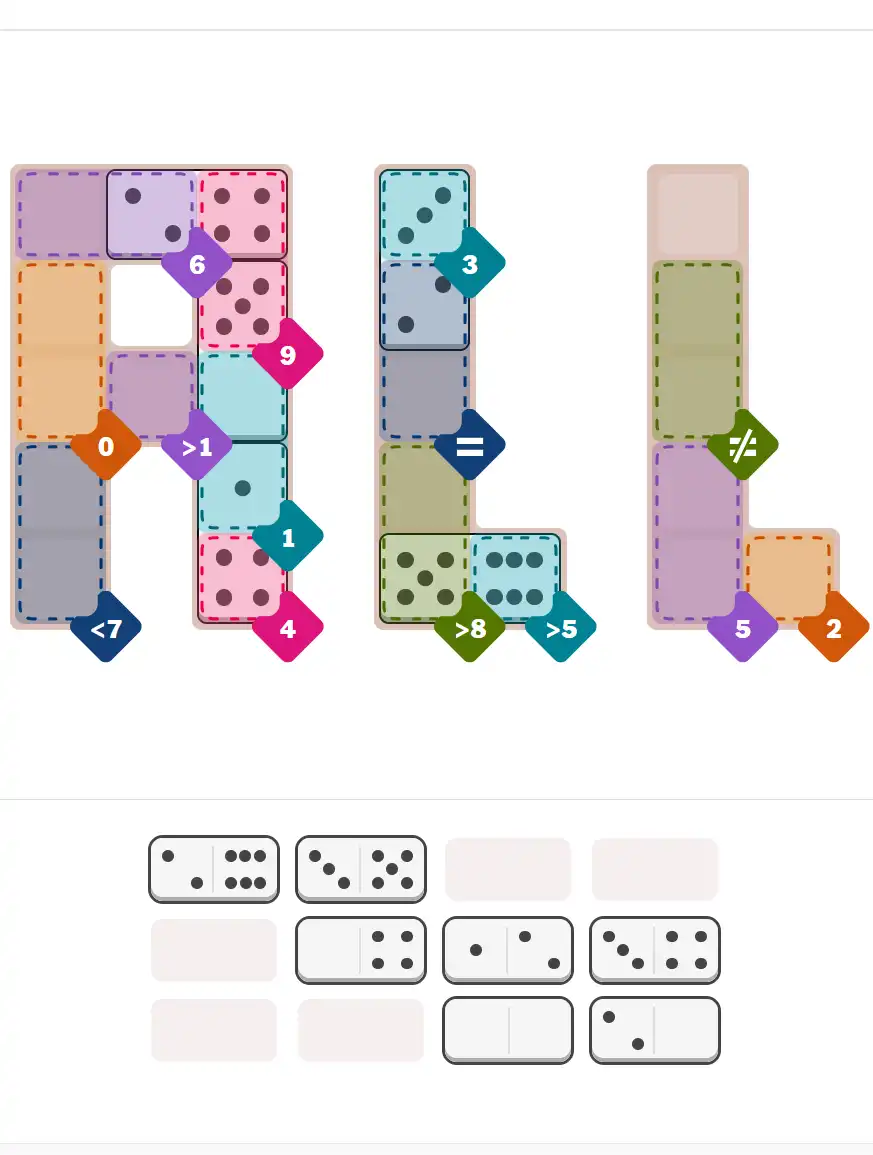
Pips hint for January 7, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

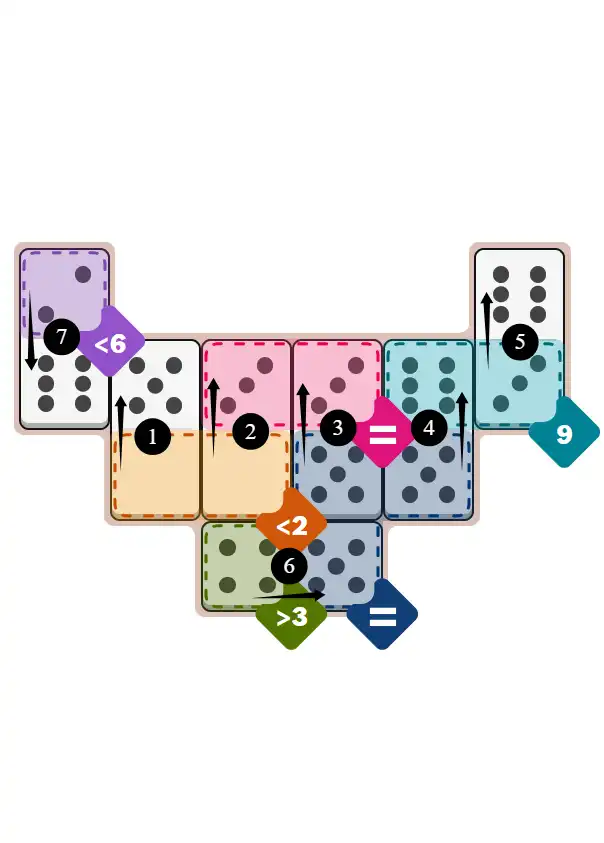
Final Answer: The Solved Grid for Hard Mode

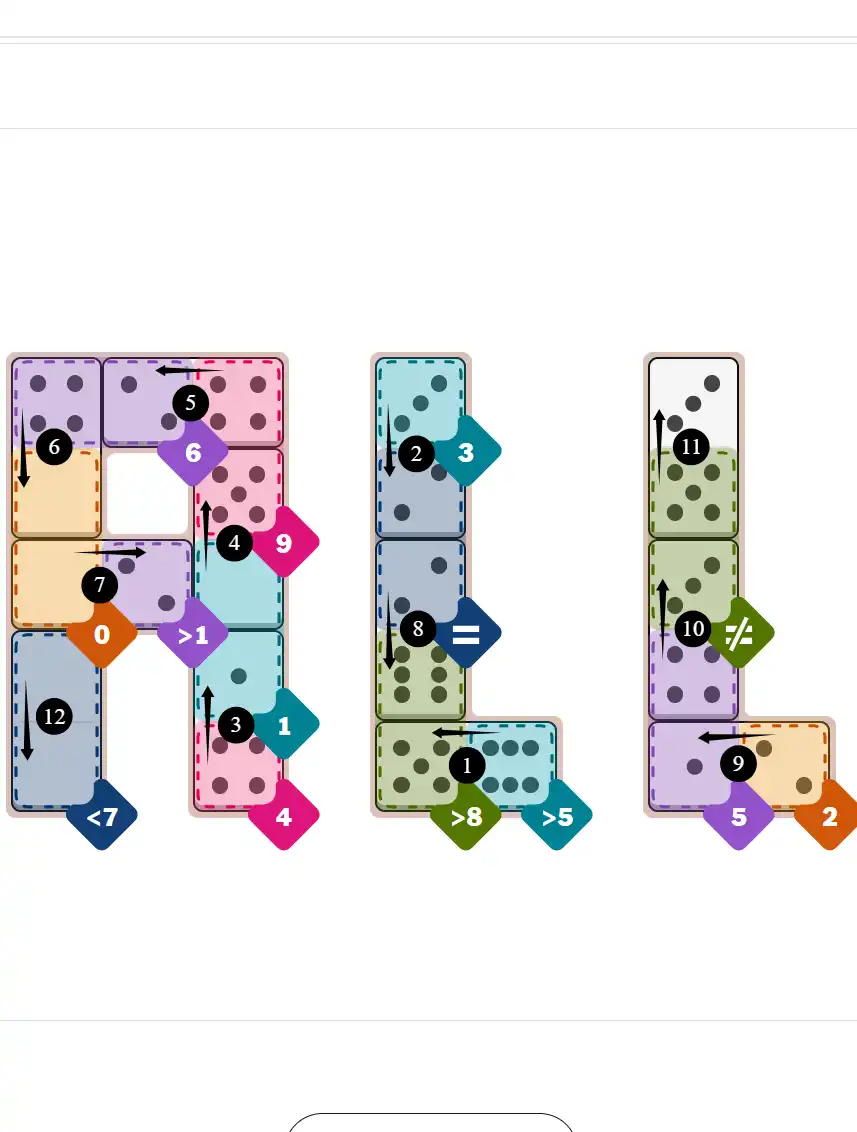
NYT Pips January 7, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [5-3], [4-2], [4-1], [3-2], [3-0].

2

Step 2: Yellow >4 + Light Blue Equal + Red Equal + Purple 7 --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 5 pips (5-3), therefore,the domino halves in Yellow >4 region must be 5. The domino halves in Light Blue Equal region must be 3. The domino halves in Red Equal region must be 2. The domino halves in Purple 7 region must be 4+3. The answer is 5-3, placed vertically; 3-2, placed horizontally; 2-4, placed horizontally; 3-0 (3 into Purple 7 region, 0 down into blank), placed vertically.

3

Step 3: Blue 4 --(Arrows ⑤)

The answer is 4-1 (4 into Blue 4 region, 1 right into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-5], [6-3], [6-2], [5-4], [5-3], [5-0], [3-0]. The smallest possible sum of the pips on a domino is 3 and the samallest pips is 2, therefore, the domino halves in Yellow <2 region must be 0+0, the domino halves in Blue Equal only left 5 or 6 can be choose.

2

Step 2: Yellow <2 + Red Equal + Blue Equal + Light Blue 9 --(Arrows ①②③④⑤)

Confirmed by neighboring region and step 1 and relative position. No domino with the same number, only 2 dominoes with 0 pips (5-0, 3-0), therefore, these two dominoes must placed vertically. The domino halves in Yellow <2 region must be 0+0. The domino halves in Red Equal region must be 3. The domino halves in Blue Equal region must be 5. The domino halves in Light Blue 9 region must be 3+6. The answer is 0-5 (5 up into blank), placed vertically; 0-3 (3 into Red Equal), placed vertically; 5-3 (3 into Red Equal), placed vertically; 5-6, placed vertically; 3-6 (3 into Light Blue 9 region, 6 up into blank), placed vertically.

3

Step 3: Green >3 + Purple <6 --(Arrows ⑥⑦)

Confirmed by neighboring region and step 2 and remaining dominoes (6-2, 4-5). The answer is 4-5 (4 into Green >3 region, 5 into Blue Equal region), placed horizontally; 2-6 (2 into Purple <6 region, 6 down into blank), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-5], [6-2], [5-3], [5-0], [4-3], [4-2], [4-1], [4-0], [3-2], [2-1], [2-0], [0-0]. Only 5 domino halves that contain 0 pips, need two for Yellow 0 region, need one for Light Blue 1 region.

2

Step 2: Light Blue >5 + Green >8 + Blue Equal + Light Blue 3 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Light Blue >5 region must be 6. Only two dominoes with 6 pips (6-5, 6-2), the domino halves in Green >8 region must sum to be more than 8. Therefore, the answer is 6-5 (5 into Green >8 region), placed horizontally, the other domino halves in Green >8 region must be more than 3 (4 or 5 or 6). Only three dominoes with 3 pips (5-3, 4-3, 3-2), the dominoes left that contain 5 pips (5-0), the dominoes left that contain 4 pips (4-3, 4-2, 4-1, 4-0), the dominoes left that contain 2 pips (6-2, 4-2). Therefore, the domino halves in Blue Equal must be 2, the answer is 3-2 (3 into Light Blue 3 region, 2 into Blue Equal region), placed vertically.

3

Step 3: Red 4 + Light Blue 1 + Red 9 + Purple 6 + Yellow 0 + Purple >1 --(Arrows ③④⑤⑥⑦)

Confirmed by neighboring region and relative position and remaining dominoes. No domino sum to be 1 or 9, only four dominoes with 0 pips (5-0, 4-0, 2-0, 0-0), only two dominoes with 1 pips (4-1, 2-1). Therefore, the domino halves in Light Blue 1 region must be 1+0, the domino halves in Red 9 region must be 5+4, the domino halves in Purple 6 region must be 2+4, the domino halves in Yellow 0 region must be 0+0 and come from two different dominoes. The answer is 4-1 (4 into Red 4 region), placed vertically; 0-5, placed vertically; 4-2 (4 into Red 9 region), placed horizontally; 4-0 (4 into Purple 6 region), placed vertically; 0-2 (2 into Purple >1 region), placed horizontally.

4

Step 4: Blue Equal + Green >8 --(Arrows ⑧)

Confirmed by neighboring region and step 2 and remaining dominoes (6-2, 5-3, 4-3, 2-1, 0-0). The answer is 2-6 (2 into Blue Equal region, 6 into Green > 8 region), placed vertically.

5

Step 5: Yellow 2 + Purple 5 + Green Not Equal --(Arrows ⑨⑩⑪)

Confirmed by neighboring region and step 2 and remaining dominoes (5-3, 4-3, 2-1, 0-0). The domino halves in Purple 5 region must be 1+4. The domino halves in Green Not Equal region must be 3+5 (different). The answer is 2-1 (2 into Yellow 2 region), placed horizontally; 4-3, placed vertically; 5-3 (3 up into blank), placed vertically.

6

Step 6: Blue <7 --(Arrows ⑫)

The answer is 0-0, placed vertically.

🎥 NYT Pips January 6, 2026 — Full Domino Logic Walkthrough & Pips Hint Analysis (Easy–Hard)

Focusing on how each region constraint narrows the field and how small pips hints snowball into confident placements.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 9, 2026

View Answer →

NYT Pips Hints & Answers for January 8, 2026

View Answer →

NYT Pips Hints & Answers for January 6, 2026

View Answer →

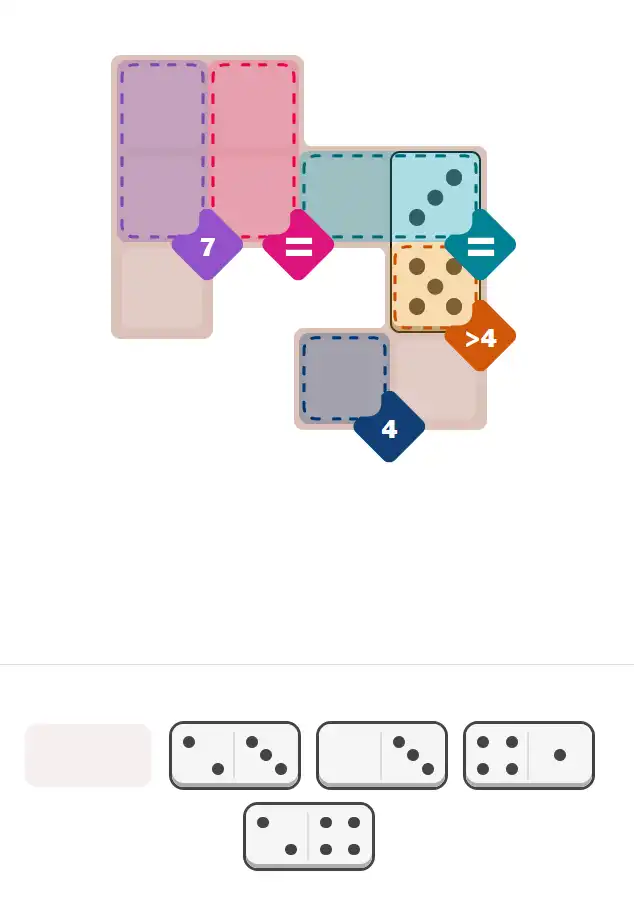
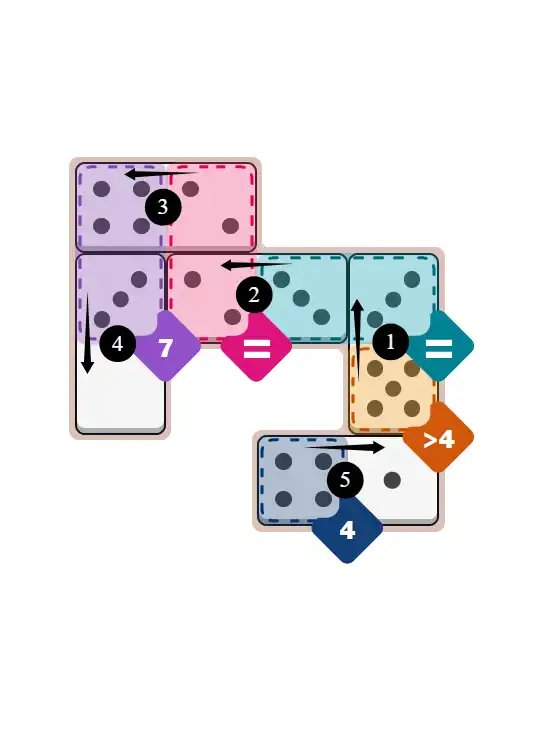
💬 Community Discussion

Leave your comment