NYT Pips Hint, Answer & Solution for February 11, 2026

Feb 11, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

NYT Pips for Wednesday, February 11, 2026 is a clean, satisfying logic test built around domino constraints, tight region rules, and the kind of deduction that rewards players who slow down and track every number carefully.

Today’s lineup features Easy (ID 595), Medium (ID 624), and Hard (ID 648)—a nicely balanced set that feels structured without being repetitive. Each grid uses a carefully limited domino pool, which means your biggest advantage isn’t speed, but awareness: spotting which tiles are rare, which totals are forced, and where a single placement can unlock multiple regions at once.

The Easy puzzle (ID 595) is a great warm-up for pattern recognition, especially if you like quick eliminations and clean sum-building logic.

The Medium puzzle (ID 624) begins to tighten the screws with more deliberate equals zones and trickier placement sequencing.

And the Hard puzzle (ID 648) is where the real payoff sits—this one rewards careful counting, domino tracking, and long-chain reasoning that feels genuinely satisfying once it clicks.

Edited by Ian Livengood, today’s release feels polished and intentional, with a smooth difficulty climb that makes it perfect for a full video walkthrough.

If you’re looking for a Pips hint today, or you want a complete NYT Pips solution breakdown by difficulty, this is one of those puzzle sets where the logic is clear—but only after you earn it.

Written by Ander

Puzzle Analyst – Sophia

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - So easy

Just do it

💡 Hint #1 - Use Pip Scarcity to Fix the Blank

Begin by counting rare pips in the domino set. Since there are only two 0-halves available and Purple 1 requires 0+0+1, both zeros are automatically reserved there. That instantly forces the 2 pip to be placed into the blank cell, narrowing the entire grid before any placements.

💡 Hint #2 - Solve Sum Regions by Hunting the Only Missing Number

For Yellow 5, the only realistic split is 1+4. Once you notice that 4 exists only once in the pool (from 6-4), the placement becomes forced. This also creates a strong domino-availability clue: if 6-4 is consumed, the connected Purple Equal region can no longer vary and must lock into 6.

💡 Hint #3 - Finish the Low-Sum Region to Trigger Inequality Deductions

After confirming Purple 1 must be 0+0+1, place the remaining zero dominoes to complete that region. This immediately determines Green <2 (must take the 1) and forces Light Blue >2 to take the only remaining high half. Completing a tiny target region early is a reliable way to activate multiple constraint zones at once.

💡 Hint #4 - Close the Puzzle by Assigning Remaining Doubles

When the board is nearly solved, shift focus to the leftover domino pool. With only (6-6), (3-3), and (5-3) remaining, the Equal regions become obvious: Blue Equal must claim the 6s, and Red Equal must claim the 3s. Using doubles to satisfy Equal zones is often the cleanest final shortcut.

💡 Hint #1 - Count Rare Pips First

Start by scanning the domino pool for scarce numbers. Here, 4s and 1s are extremely limited, so any region demanding those values becomes a priority. This kind of pip-counting immediately narrows which regions can realistically take certain halves and prevents wasted placements.

💡 Hint #2 - Force Equals Zones with a Mandatory Pip

When a blank cell must contain a specific pip (like the only available 1), use that requirement to lock down nearby Equal regions. If one number is forced outside the Equal zone, the Equal zone often collapses into a single possible value, creating an early chain reaction.

💡 Hint #3 - Lock Down Zeros to Control the Board

Once a 0 is confirmed in an Equal region, treat it like a board anchor. Zero-based equals zones sharply restrict tile choices and make it easier to assign remaining high-value dominoes to other regions without guessing.

💡 Hint #4 - Solve Multiple Equals Regions as a Package

When several Equal regions touch or interact, solve them together instead of separately. Use remaining domino availability to decide which equal-value is still possible, then place tiles that satisfy multiple regions at once to quickly reduce the domino pool.

💡 Hint #5 - Clean Up with the Last Unused Pair

In the endgame, check what domino is still unused and see which region has only one value left to accept. Once the surrounding Equal regions are fixed, the final placement is usually a simple leftover confirmation rather than a new deduction.

🎨 Pips Solver

Feb 11, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

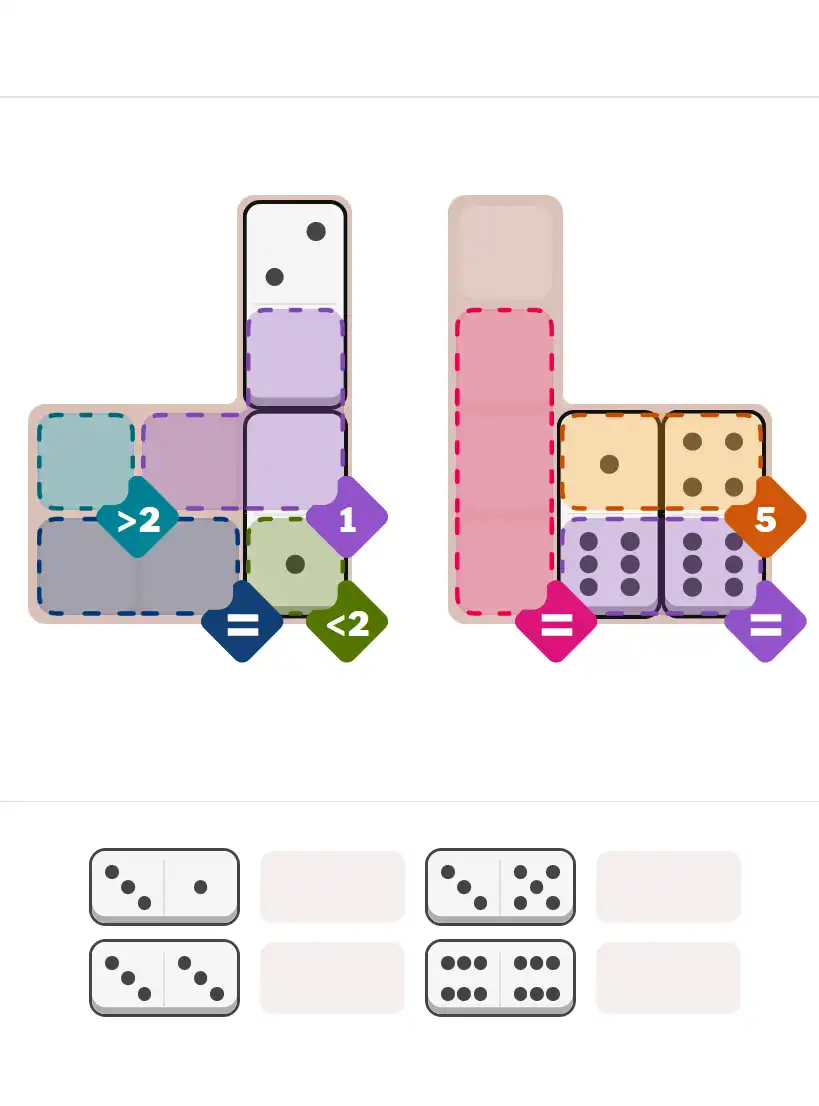
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

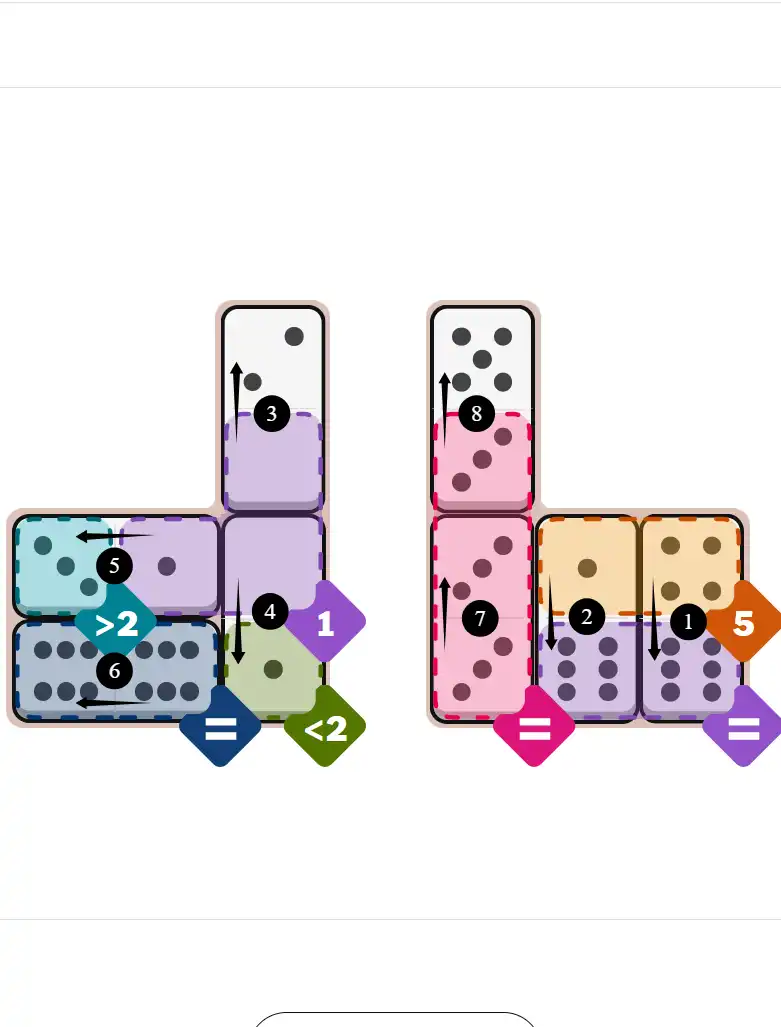
Starting Position & Key First Steps

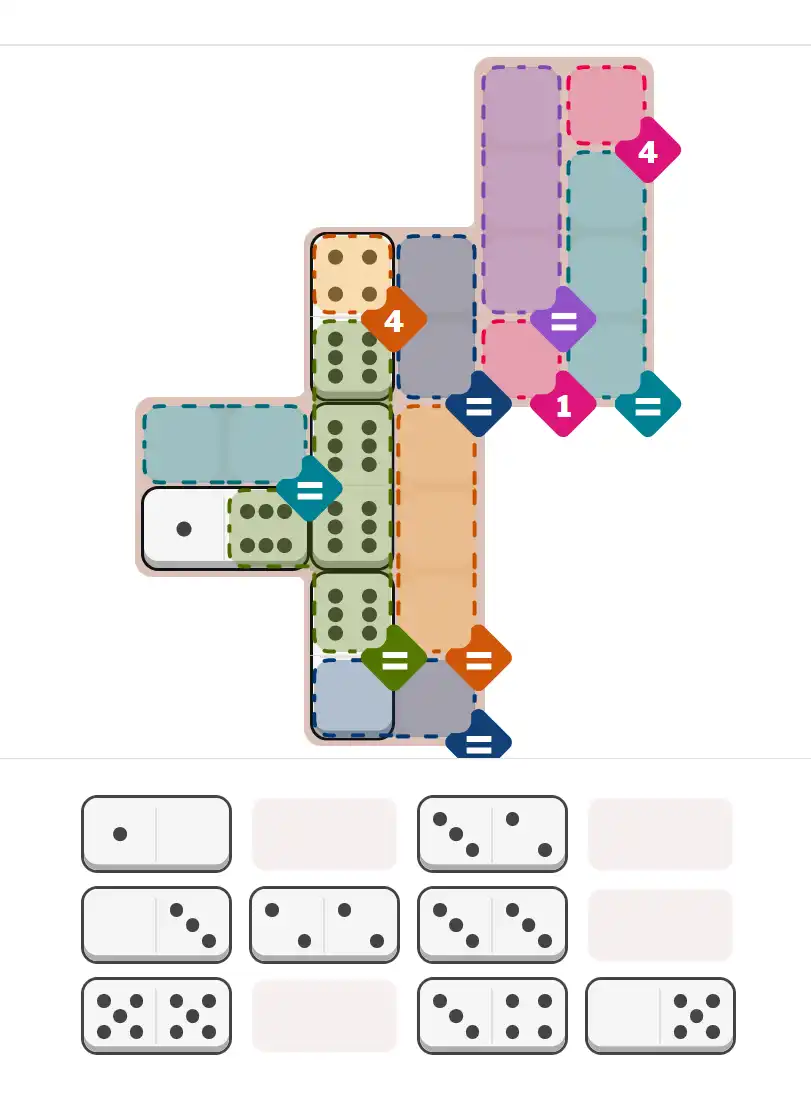
Pips hint for February 11, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

Final Answer: The Solved Grid for Hard Mode

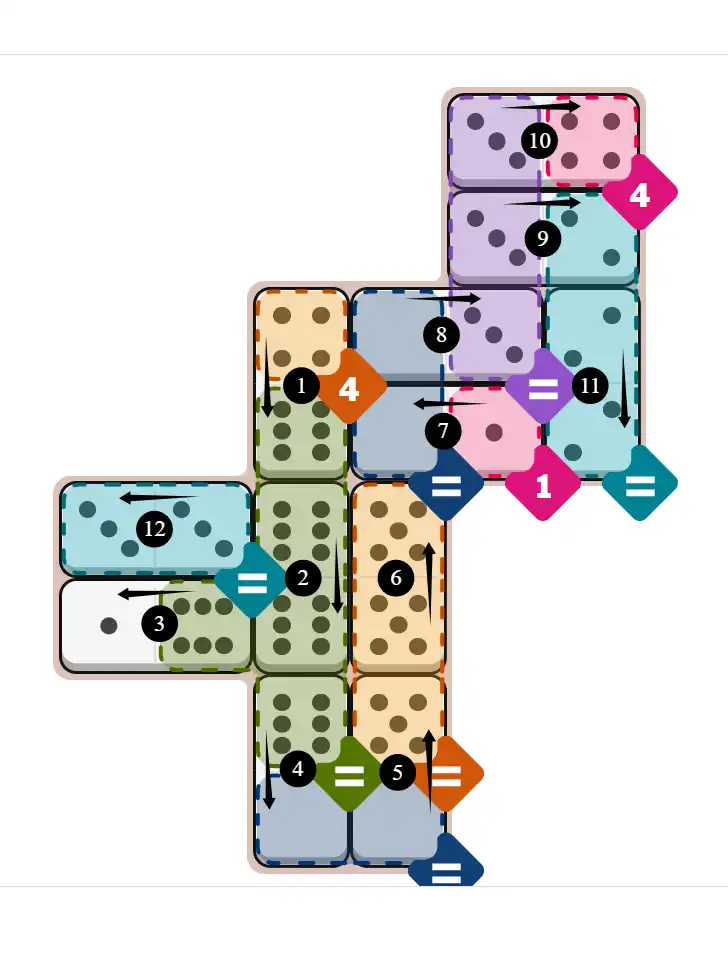
NYT Pips February 11, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-2], [5-0], [4-2], [2-1], [0-0].

2

Step 2: Light Blue Equal + Red 11 + Purple 4 --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Light Blue Equal region must be 0. The domino halves in Red 11 must be 5+6. The domino halves in Purple 4 region must be 2+2. The answer is 0-0, placed vertically; 0-5, placed horizontally; 6-2, placed vertically; 2-1 (1 down into blank), placed vertically.

3

Step 3: Yellow >3 --(Arrows ⑤)

The answer is 4-2 (4 into Yellow >3 region, 2 up into blank), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [6-4], [6-1], [5-3], [3-3], [3-1], [2-0], [1-0]. The domino halves in Purple 1 region must be 0+0+1. Only 2 domino halves that contain 0 pips (2-0, 1-0) for Purple 1 region, 2 pips must placed in blank.

2

Step 2: Yellow 5 + Purple Equal --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Yellow 5 region must be 1+4. Only one domino with 4 pips (6-4), so the domino halves in Purple Equal region must be 6. The answer is 4-6, placed vertically; 1-6, placed vertically.

3

Step 3: Purple 1 + Green <2 + Light Blue >2 --(Arrows ③④⑤)

Confirmed by all left regions and remaining dominoes. The domino halves in Light Blue 1 region must be 0+0+1. The answer is 0-2 (2 up into blank), placed vertically; 0-1 (1 into Green <2 region), placed vertically; 1-3 (3 into Light Blue >2 region), placed horizontally.

4

Step 4: Blue Equal + Red Equal --(Arrows ⑥⑦⑧)

Confirmed by neighboring region and remaining dominoes (6-6, 5-3, 3-3). The domino halves in Blue Equal must be 6. The domino halves in Red Equal must be 3. The answer is 6-6, placed horizontally; 3-3, placed vertically; 3-5 (5 up into blank), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-6], [6-4], [6-1], [6-0], [5-5], [5-0], [4-3], [3-3], [3-2], [3-0], [2-2], [1-0]. Only 2 domino halves that contain 4 pips (6-4, 4-3) for Red 4 region and Yellow 4 region. Only 2 domino halves that contain 1 pips (6-1, 1-0), need one for Red 1 region. Only 5 domino halves that contain 6 pips (6-6, 6-4, 6-1, 6-0), only 5 domino halves that contain 3 pips.

2

Step 2: Yellow 4 + Green Equal --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. Need one 1s must placed in blank, therefore, the domino halves in Green Equal region must be 6. The answer is 4-6 (4 into Yellow 4 region), placed vertically; 6-6, placed vertically; 6-1 (1 left into blank), placed horizontally; 6-0 (0 down into Bottom Blue Equal region), placed vertically.

3

Step 3: Bottom Blue Equal + Yellow Equal --(Arrows ⑤⑥)

Confirmed by neighboring region and step 1 and remaining dominoes. The domino halves in Blue Equal must be 0 (one 0s already come from Arrows ④). The domino halves in Yellow Equal must be 5. The answer is 0-5, placed vertically; 5-5, placed vertically.

4

Step 4: Red 1 + Top Blue Equal + Purple Equal + Red 4 + Right Light Blue Equal --(Arrows ⑦⑧⑨⑩⑪)

Confirmed by neighboring region and remaining dominoes (4-3, 3-3, 3-2, 3-0, 2-2, 1-0). The domino halves in Top Blue Equal must be 0. The domino halves in Purple Equal must be 3. The domino halves in Right Light Blue Equal region must be 2. The answer is 1-0, placed horizontally; 0-3, placed horizontally; 3-2, placed horizontally; 3-4 (4 into Red 4 region), placed horizontally; 2-2, placed vertically.

5

Step 5: Left Light Blue Equal --(Arrows ⑫)

The answer is 3-3, placed horizontally.

🎥 NYT Pips February 11, 2026 (Wednesday) – Full Solutions & Pips Hint Today (Easy 595 / Medium 624 / Hard 648)

This walkthrough covers the full logic path—no guessing, just deductions.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for February 12, 2026

View Answer →

NYT Pips Hints & Answers for February 10, 2026

View Answer →

NYT Pips Hints & Answers for February 9, 2026

View Answer →

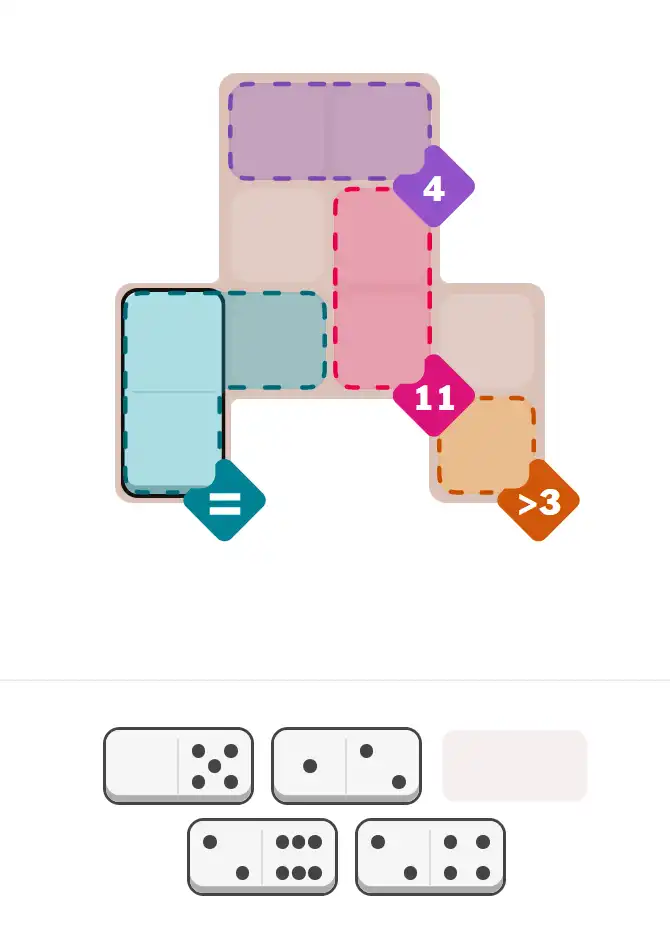
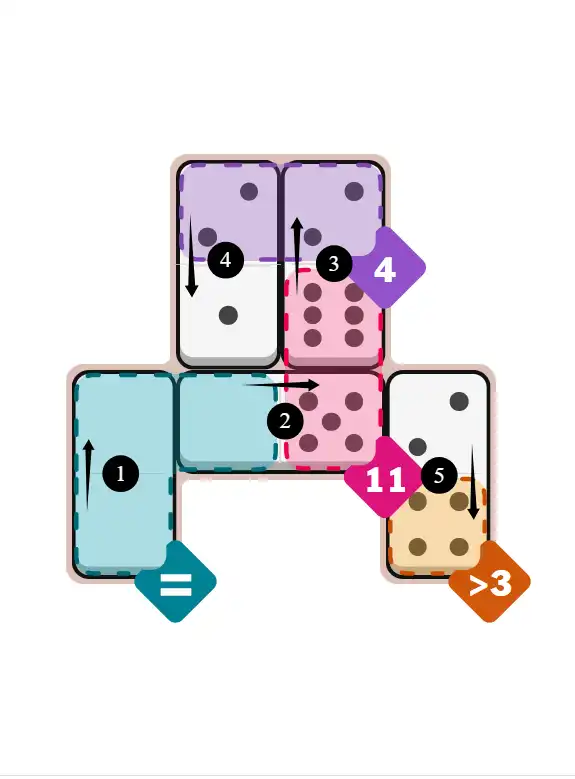
💬 Community Discussion

Leave your comment