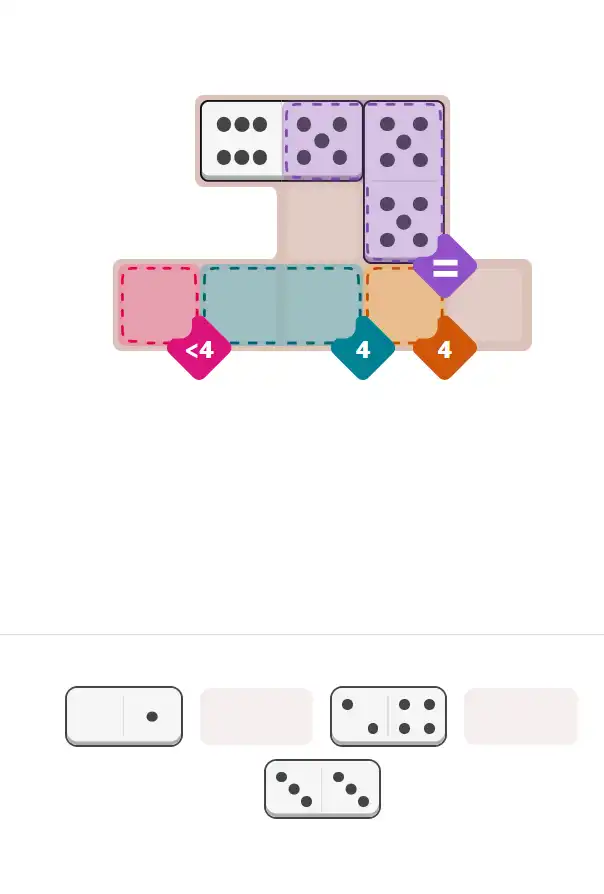
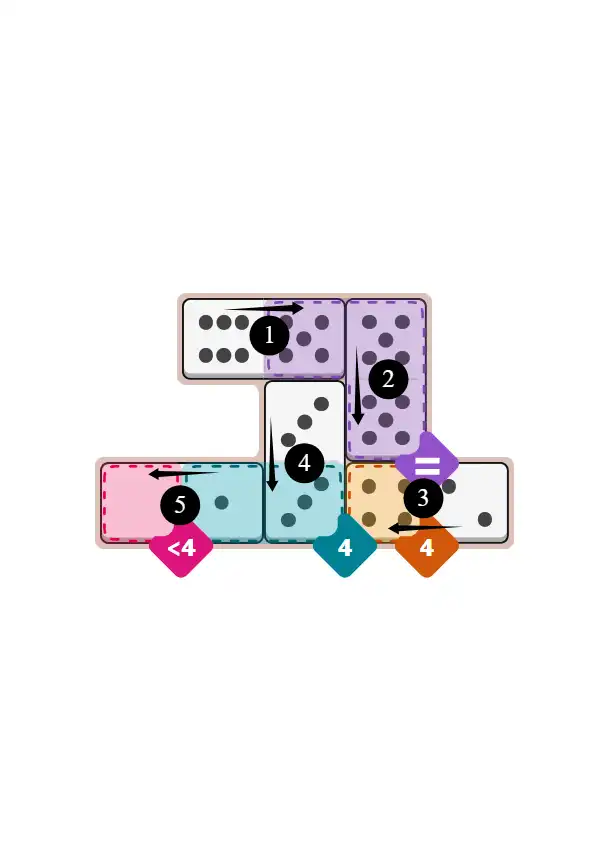
🔧 Step-by-Step Answer Walkthrough For Easy Level
Today's set: 6-5, 5-5, 4-2, 3-3, 1-0. Spot the pattern: you have three domino halves with 5-pips (6-5 and both sides of 5-5). This screams 'equal region!' Pips hint: when you see multiple copies of the same number, check for equal regions first.
This region needs all matching halves. You've got exactly three 5-pips available—perfect match! Place 6-5 horizontally and 5-5 vertically, all showing 5s in this region. Pips puzzle tip: doubles like 5-5 are gold in equal regions since both sides automatically match.
This region needs pips totaling 4. Looking at remaining dominoes: 4-2, 3-3, 1-0. The 4-2 domino placed horizontally contributes its 4-side perfectly here. Quick and clean. Pips NYT puzzle wisdom: when one domino half exactly matches a sum target, that's usually your answer.
Another region wanting 4 total. With 3-3 and 1-0 left, the solution is 3+1=4. Place 3-3 vertically and 1-0 horizontally, combining to hit the target. Done! Pips hint: the last pieces should confirm your earlier placements—if they don't fit, backtrack to Step 2.
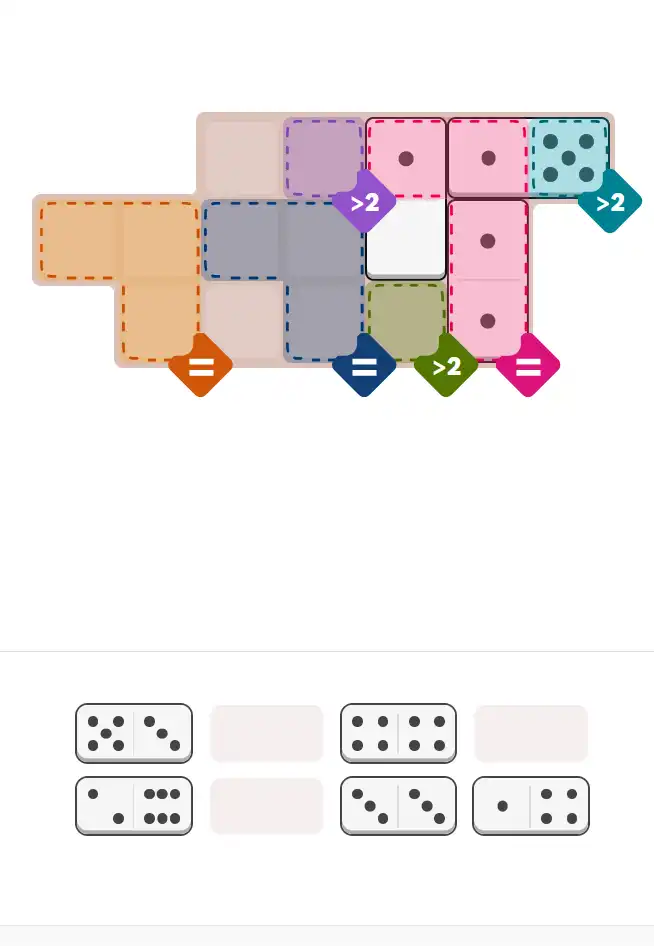
🔧 Step-by-Step Answer Walkthrough For Medium Level
Dominoes: 6-2, 5-3, 5-1, 4-4, 4-1, 3-3, 1-1, 1-0. Key observation: only 5 domino halves contain 1-pips total. The Pink Equal region needs 4 matching halves. Here's the trick—you have one 4-1 domino that contains both a 4 and a 1. If you use 4-1 in the Pink Equal region, you'd need its 1-side, but then the Orange Equal region (needing 4s) would lose a critical 4-pip. Only 3 domino halves have 4-pips, so you can't spare it. Pips hint: when a domino contains two scarce resources, figure out which region needs it more.
From Step 1, we must exclude 4-1 from this region to preserve 4-pips for the Orange Equal. That leaves exactly 4 domino halves with 1-pips: from 5-1, 1-1, and 1-0. Place 5-1 horizontally, 1-1 vertically, and 1-0 vertically—all showing 1s in the Pink region. Pips NYT puzzle tip: when scarcity forces exclusions, count what remains and verify it's enough.
With Pink solved, check remaining dominoes: 6-2, 5-3, 4-4, 4-1, 3-3. The Dark Blue Equal needs matching halves. You've got two dominoes with 3-pips: 5-3 and 3-3. Place both horizontally, showing their 3-sides in this region. Pips hint: equal regions in medium puzzles often use exactly all available copies of one number.
Now the 4-1 domino earns its keep! This region needs matching 4-pips. Place 4-4 horizontally and 4-1 horizontally, both contributing 4s here. This is why we couldn't use 4-1 in the Pink region earlier—we needed its 4-side here. Pips puzzle wisdom: strategic placement means thinking two steps ahead about where scarce pips must ultimately go.
Last domino: 6-2. The Purple region needs all pips greater than 2. Place 6-2 horizontally—the 6 obviously satisfies >2. Done! Pips NYT puzzle tip: 'greater than' constraints are usually solved last since they're flexible about which high-pip dominoes to use.
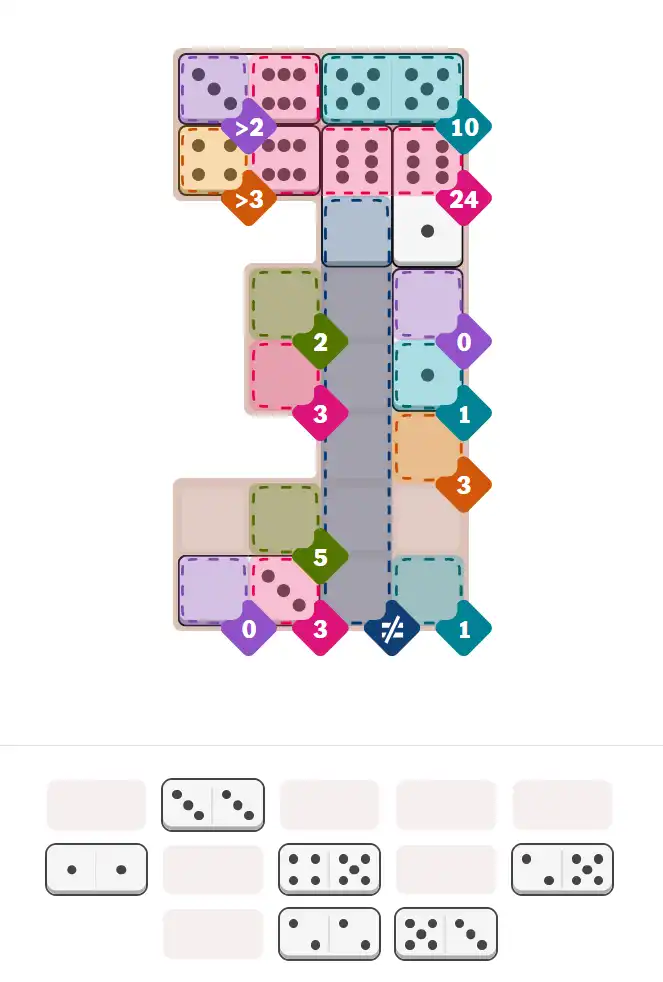
🔧 Step-by-Step Answer Walkthrough For Hard Level
Dominoes: 6-4, 6-3, 6-1, 6-0, 5-5, 5-4, 5-3, 5-2, 3-3, 3-0, 2-2, 1-1, 1-0. Critical observation: only 4 domino halves contain 6-pips, and the Pink Number 24 region will consume all of them (6+6+6+6=24). This severe scarcity dictates your entire solve path. Pips hint: in hard puzzles, always count your rarest resource first—it's your constraint anchor.
This region needs exactly 10 pips. The 5-5 double placed horizontally hits the target perfectly in one domino. Easy decision. Pips NYT puzzle tip: when a double matches a sum region exactly, place it immediately—it frees up your mental workspace for harder decisions.
From Step 1, we know all four 6-pips must go here (6×4=24). Place 6-4 horizontally, 6-3 horizontally, 6-0 vertically (confirmed by Steps 4 and 9 which need the 0), and 6-1 vertically. The non-6 sides (4, 3, 0, 1) extend into neighboring regions—we'll use them strategically. Pips puzzle wisdom: committing scarce resources early creates clarity, not chaos.
This region demands all different pip values. With dominoes bordering from Step 3, we need to fill this with 0, 1, 2, 3, 4, 5—all distinct. This constraint will guide our next several placements. Pips hint: 'not equal' regions in hard puzzles force you to balance resource allocation across multiple neighboring sum regions.
No dominoes have a 2-3 combination available. Looking at remaining pieces and the Not Equal constraint from Step 4, place 0-1 vertically. The 0 satisfies the Purple region, the 1 satisfies the Teal region, and both contribute to the Not Equal diversity. Pips NYT puzzle strategy: when dominoes serve multiple regions simultaneously, prioritize them.
Only 3 dominoes contain 3-pips remaining. Checking all the Number 3 regions on the board, place 0-3 horizontally here. The 0 completes another 0-region, while the 3 contributes to a 3-region. Pips hint: when a pip value is scarce (like 3s), map out ALL regions needing it before committing.
Continuing with our 3-pip allocation from Step 6, place 5-3 horizontally and 3-3 horizontally. These satisfy the two remaining 3-regions. The 5s extend into other areas we'll address shortly. Pips puzzle tip: clustering similar constraints (multiple 3-regions) and solving them together prevents backtracking.
From Step 7's placements, check remaining dominoes with 2-pips. Place 2-2 horizontally in this region. The double-2 efficiently handles this sum constraint. Pips hint: after solving clustered regions, the remaining pieces often have obvious homes.
Last three dominoes: 1-1, 5-4, 5-2. Place 1-1 horizontally (satisfying the Teal 1 region), 5-4 horizontally (contributing 5 to the Green region and 4 to complete the Not Equal diversity), and 5-2 horizontally (adding 5+2 to the Green 5 region). Everything clicks into place. Pips NYT puzzle wisdom: if your final placements don't fit seamlessly, something went wrong at Step 3 or 4—backtrack to the scarcity decisions.


💬 Community Discussion
Leave your comment