NYT Pips Hint, Answer & Solution for December 31, 2025

Dec 31, 2025

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Join the community challenge for the Daily Domino Puzzle on Wednesday, December 31, 2025, a thoughtful way to mark the final day of the year with calm focus and shared curiosity. As New Year’s Eve arrives, today’s puzzle offers a welcome pause — a chance to reflect, reset, and enjoy logic alongside players from around the world.

With easy, medium, and hard grids available, everyone can take part at their own pace. Trade ideas, swap hints, and compare solutions as the grid slowly comes together. A useful pips hint today: notice how repeated pip values compete across equal and sum regions — understanding where those pips cannot go often reveals where they must go.

What makes this end-of-year puzzle special is the sense of collaboration. Those final deductions, the moment when the last domino locks into place, feel even better when shared with the community. It’s less about racing to finish and more about enjoying the reasoning process together.

Edited by Ian Livengood, and featuring puzzles crafted by Ian Livengood (easy) and Rodolfo Kurchan (medium and hard), this New Year’s Eve challenge highlights clean design and human logic. Whether you’re checking a solution, looking for subtle hints, or simply enjoying one last puzzle before the clock strikes midnight, December 31 is a satisfying way to close the year — one pip at a time.

Written by Anna

Puzzle Analyst – Nikki

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - A piece of cake

Just do it.

💡 Hint #1 - Early Equal-Region Filtering

Start by narrowing equal regions to only values that can physically fit. When two equal regions share the same limited candidates, exclude all other pips early. This immediately forces sum regions, like Yellow 7, into a single viable combination.

💡 Hint #2 - Single-Pip Domino Forcing

When a required pip appears on only one domino, that domino becomes a hard constraint. Use it to lock both an equal region and a sum region at the same time, fixing orientations and reducing uncertainty across the grid.

💡 Hint #3 - Composite Sum Decomposition

Break larger sums into realistic pip groups based on what remains. If a sum like 11 can only be formed by a specific mix of pips, confirm it by eliminating higher or lower alternatives and place the matching domino immediately.

💡 Hint #4 - Resolve Remaining Equal Regions

Once higher-value equal regions are fixed, the remaining equal region usually collapses to a single pip. Assign it confidently, using the leftover dominoes to satisfy orientation and adjacency without creating conflicts.

💡 Hint #5 - Clean Up with Zeros

Leave zero-heavy dominoes for last. Zeros are flexible early on but become definitive once all other pips are placed, making them ideal for filling blank or unconstrained spaces at the end.

💡 Hint #1 - Pip Demand vs Supply Lock

Start by comparing how many times a pip value is required versus how many times it actually exists. Here, almost all 3-pips are consumed by equal and fixed regions, which immediately forces other equal regions to avoid 3s and reveals mandatory placements like the 5–4 domino bridging two equal regions.

💡 Hint #2 - Impossible Pair Elimination

Look for sums that cannot be formed because a specific pip pair does not exist. The absence of a 5–2 domino removes an entire branch of possibilities, forcing the remaining values into their only valid orientations across adjacent regions.

💡 Hint #3 - Equal Regions Decide High Pips

When large equal regions are fixed to a single pip, use inequality regions to decide where higher values must go. Values that exceed constraints (>1, >2) naturally push 6s, 5s, and 4s into specific equal regions, collapsing multiple regions at once.

💡 Hint #4 - Finish with Residual Sums

Leave straightforward sum regions for last. Once all competing pips are placed, the remaining dominoes usually fit uniquely. Final sums like 12 and 5 resolve cleanly when no alternative pip distributions remain.

🎨 Pips Solver

Dec 31, 2025

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

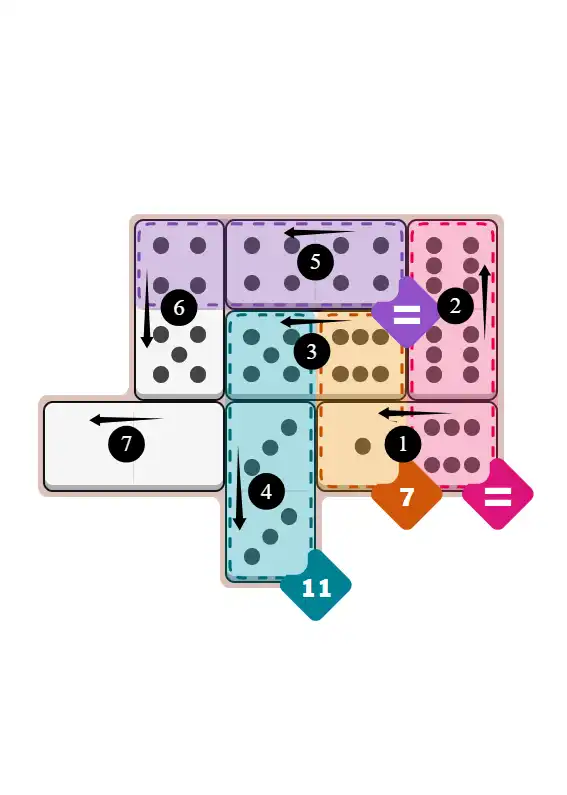
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

Starting Position & Key First Steps

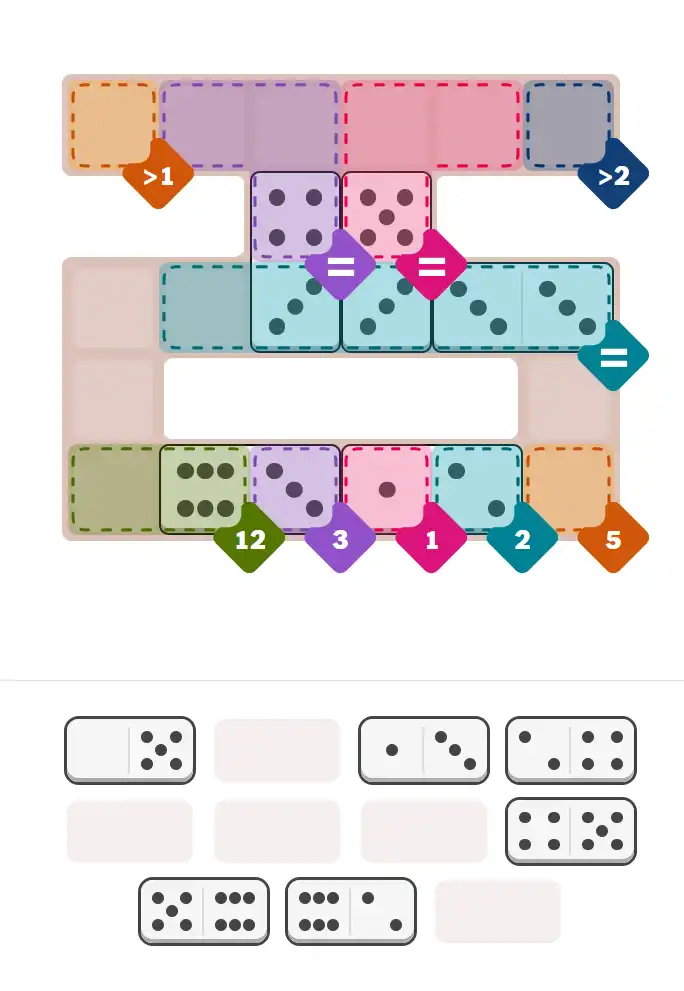
Pips hint for December 31, 2025 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

Final Answer: The Solved Grid for Hard Mode

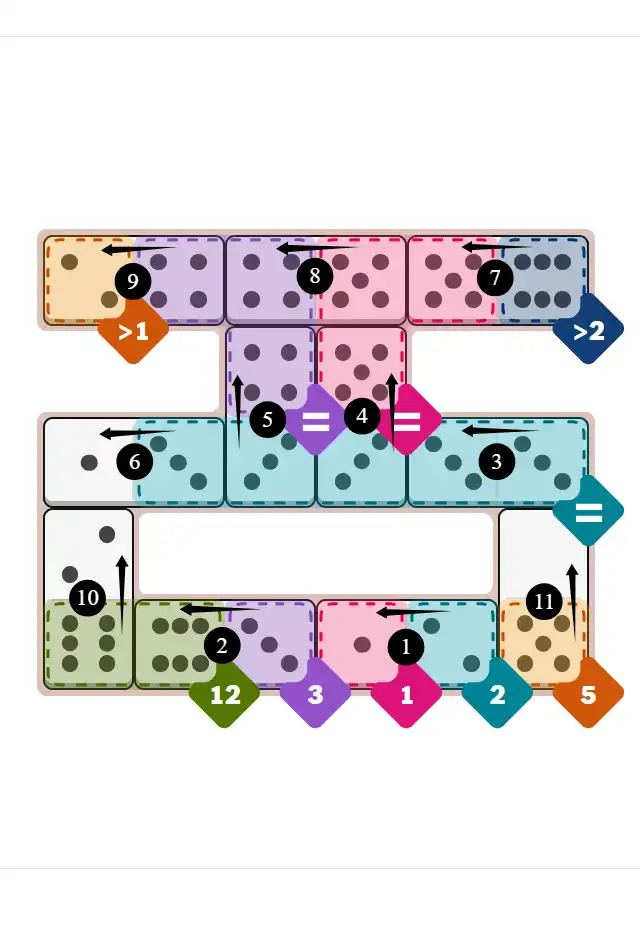
NYT Pips December 31, 2025 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-3], [6-2], [6-0], [5-1], [4-4], [3-3]. The change in the region's color does not affect the final result.

2

Step 2: Blue 3 + Yellow 18 + Red 7 --(Arrows ①②③④)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Yellow 18 region must be 6+6+6. The domino halves in Red 7 region must be 2+5. The answer is 3-6 (3 into Blue 3 region), placed horizontally; 6-2, placed horizontally; 5-1 (1 up into blank), placed vertically; 6-0 (0 right into blank), placed horizontally.

3

Step 3: Light Blue 8 + Purple Equal --(Arrows ⑤⑥)

Confirmed by neighboring region and remaining dominoes (4-4, 3-3). The answer is 4-4 (whole domino into Light Blue 8 region), placed horizontally; 3-3 (whole domino into Purple Equal region), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [6-5], [6-1], [5-4], [4-4], [3-3], [0-0]. The domino halves in Red Equal region and Purple Equal region must be 6 or 4. The domino halves in Yellow 7 region must be 1+6. The change in the region's color does not affect the final result.

2

Step 2: Red Equal + Yellow 7 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 1 pips (6-1). The domino halves in Red Equal region must be 6. The domino halves in Yellow 7 region must be 1+6. The answer is 6-1 (6 into Red Equal region, 1 into Yellow 7 region), placed horizontally; 6-6 (whole domino into Red Equal region), placed vertically; 6-5 (6 into Yellow 7 region, 5 into Light Blue 11 region), placed horizontally.

3

Step 3: Light Blue 11 --(Arrows ④)

Confirmed by neighboring region and step 2 and remaining dominoes (5-4, 4-4, 3-3, 0-0). The domino halves in this region must be 5+3+3 (5s come from step 2). The answer is 3-3 (whole domino), placed vertically.

4

Step 4: Purple Equal --(Arrows ⑤⑥)

Confirmed by neighboring region and remaining dominoes (5-4, 4-4, 0-0). The domino halves in this region must be 4. The answer is 4-4, placed horizontally; 4-5 (5 down into blank), placed vertically.

5

Step 5: Left Blank --(Arrows ⑦)

The answer is 0-0, placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-5], [6-3], [6-2], [5-4], [5-3], [5-0], [4-3], [4-2], [3-3], [3-1], [2-1]. Only 6 domino halves that contain 3 pips, need five for Light Blue Equal, need one for Purple 3 region. The domino halves in Red Equal region and Purple Equal region must be 5 or 4, [5-4] must placed in the boundary between Red Equal region and Purple Equal region. The domino halves in Green 12 must be 6+6. The change in the region's color does not affect the final result.

2

Step 2: Light Blue 2 + Red 1 + Purple 3 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. No domino with the number 5-2. Therefore, the answer is 2-1, placed horizontally; 3-6 (6 left into Green 12 region), placed horizontally.

3

Step 3: Light Blue Equal + Red Equal + Blue >2 + Purple Equal + Yellow >1 --(Arrows ③④⑤⑥⑦⑧⑨)

Confirmed by neighboring region and step 1 and remaining dominoes (6-5, 6-2, 5-4, 5-3, 5-0, 4-3, 4-2, 3-3, 3-1). The domino halves in Light Blue Equal region must be 3. 6s from the domino [6-5] more than 2, 2s from the domino [4-2] more than 1. Therefore, the domino halves in Red Equal region must be 5, the domino halves in Purple Equal region must be 4. The answer is 3-3, placed horizontally; 3-5 (5 into Red Equal region), placed vertically; 3-4 (4 into Purple Equal region), placed vertically; 3-1 (1 left into blank), placed horizontally; 6-5 (6 into Blue >2 region), placed horizontally; 5-4, placed horizontally; 4-2 (2 into Yellow >1 region), placed horizontally.

4

Step 4: Green 12 + Yellow 5 --(Arrows ⑩⑪)

Confirmed by neighboring region and remaining dominoes (6-2, 5-0). The answer is 6-2 (6 into Green 12 region, 2 up into blank), placed vertically; 5-0 (5 into Yellow 5 region, 0 up into blank), placed vertically.

🎥 Easy–Hard Logic Breakdown with Real Pips Insights

Enjoy slowing down and understanding the logic, not just finishing

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 1, 2026

View Answer →

NYT Pips Hints & Answers for December 30, 2025

View Answer →

NYT Pips Hints & Answers for December 29, 2025

View Answer →

💬 Community Discussion

Leave your comment