NYT Pips Hint, Answer & Solution for January 16, 2026

Jan 16, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

On Friday, January 16, 2026, NYT Pips lands right at the end of the workweek with a clean, data-driven logic workout that feels especially satisfying to dig into.

It’s the kind of Friday puzzle session where you slow down, recheck assumptions, and enjoy that moment when the numbers finally line up.

Edited by Ian Livengood, today’s set emphasizes efficiency, constraint management, and disciplined domino placement.

Every grid rewards careful counting and forward planning, making this a great day for players who enjoy structured reasoning and measurable progress.

The Easy puzzle (ID 520) keeps things sharp and approachable.

A compact domino set combined with multiple equals regions creates a fast logic check that highlights accurate counting and early elimination—perfect for sharing a quick Pips Hint or warming up before the tougher grids.

The Medium puzzle (ID 544), constructed by Rodolfo Kurchan, raises the bar with unequal regions and tightly bounded targets.

Here, casual guessing quickly falls apart, and success comes from tracking remaining dominoes and testing placements with intent—an ideal puzzle for mid-solve analysis and discussion.

At the top end, the Hard puzzle (ID 566) delivers a serious challenge.

Large sum requirements, wide equal zones, and subtle zero-sum traps combine to leave very little room for error. This is where careful sequencing matters, and where a well-timed pips hint today can save minutes of backtracking.

Whether you’re reviewing solutions, refining your logic, or benchmarking your solving performance, January 16, 2026 offers a focused NYT Pips experience that feels tailor-made for serious solvers heading into the weekend.

Written by Nikki

Puzzle Analyst – Mark

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - Observe

Dominoes Include: [6-4], [5-0], [4-3], [3-2], [2-2], [0-0]. Only 2 dominoes with the same number (2-2, 0-0) for Light Blue Equal region and Purple Equal region.

💡 Hint #1 - Break Regions by Domino Diversity

Start by checking regions that require halves from different dominoes. This immediately limits combinations and reveals that Light Blue 7 can only be formed as 2+2+3, forcing the double-3 onto a critical boundary.

💡 Hint #2 - Use Scarce Pips to Anchor Placement

When a region needs rare pips, place those dominoes first. With only two 2-pip dominoes and one 3-pip domino available, Light Blue 7 becomes fixed and Yellow >4 is resolved by orientation.

💡 Hint #3 - Resolve Not-Equal Regions by Full Coverage

For a Not Equal region spanning many cells, identify the complete set of distinct values it must contain. Here, Purple Not Equal must use 3, 4, 5, and 6 exactly once, making placements deterministic.

💡 Hint #4 - Finish with the Only Valid Threshold Fit

Threshold regions like Red <11 often collapse at the end. Once higher values are committed elsewhere, the remaining domino that safely fits the limit becomes the forced solution.

💡 Hint #1 - Count High-Value Pips Early

Start by counting scarce high pips. With only four 6-pip halves available, the Light Blue 24 region must be filled entirely by 6s, which immediately constrains several other regions and fixes the composition of Green Not Equal.

💡 Hint #2 - Lock Forced Totals First

When a large sum region has an exact total and limited candidates, commit to it early. Filling Light Blue 24 with four 6s resolves Red 1 and forces the orientation of nearby purple regions.

💡 Hint #3 - Use Singleton Pips to Fix Equals Regions

When only one domino remains with a specific pip (here, pip 1), equals regions become fixed. Use that scarcity to determine the value of the entire equals region and cascade placements outward.

💡 Hint #4 - Resolve Heavy Sum Regions Before Fine Details

Large regions like Purple 20 narrow the puzzle dramatically. Once most 5s are committed, smaller sum regions (like Yellow 5 and Light Blue 5) can be solved by simple partitioning of the remaining pips.

💡 Hint #5 - Finish Not-Equal Regions by Exhaustion

For Not Equal regions requiring a full set of distinct values, place remaining dominoes by elimination. Once all other regions are fixed, the not-equal constraint becomes deterministic.

💡 Hint #6 - Close with the Only Possible Fit

At the endgame, leftover dominoes often have only one legal home. Here, the final Purple 10 region accepts only a domino summing to 6, making the last placement automatic.

🎨 Pips Solver

Jan 16, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

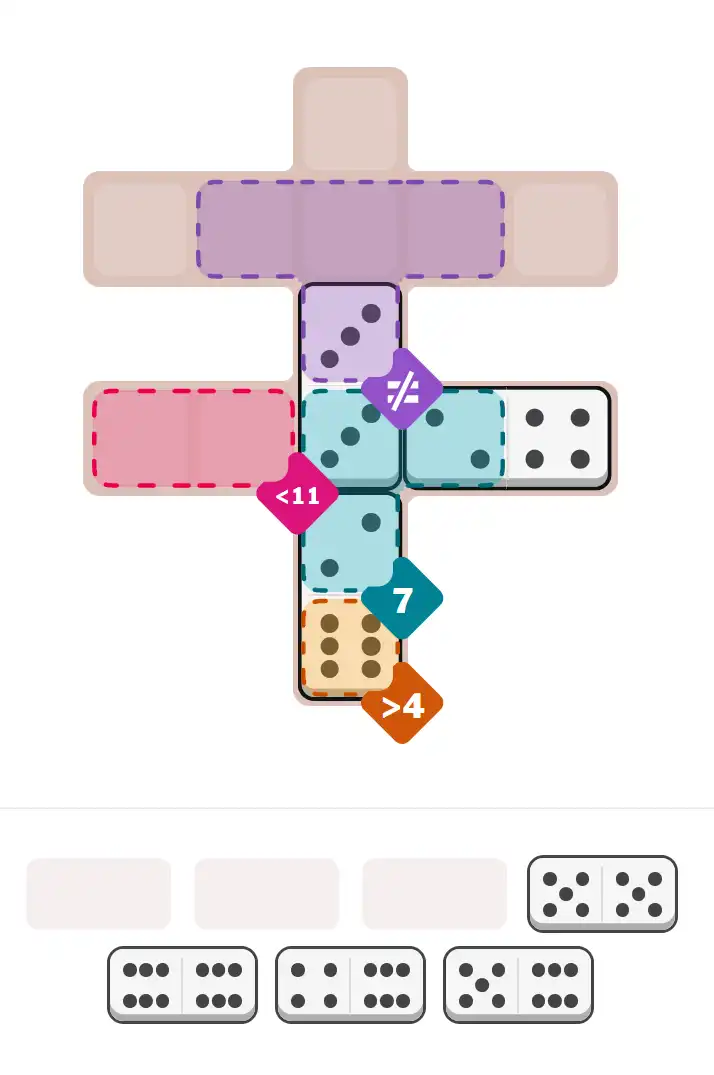
Starting Position & Key First Steps

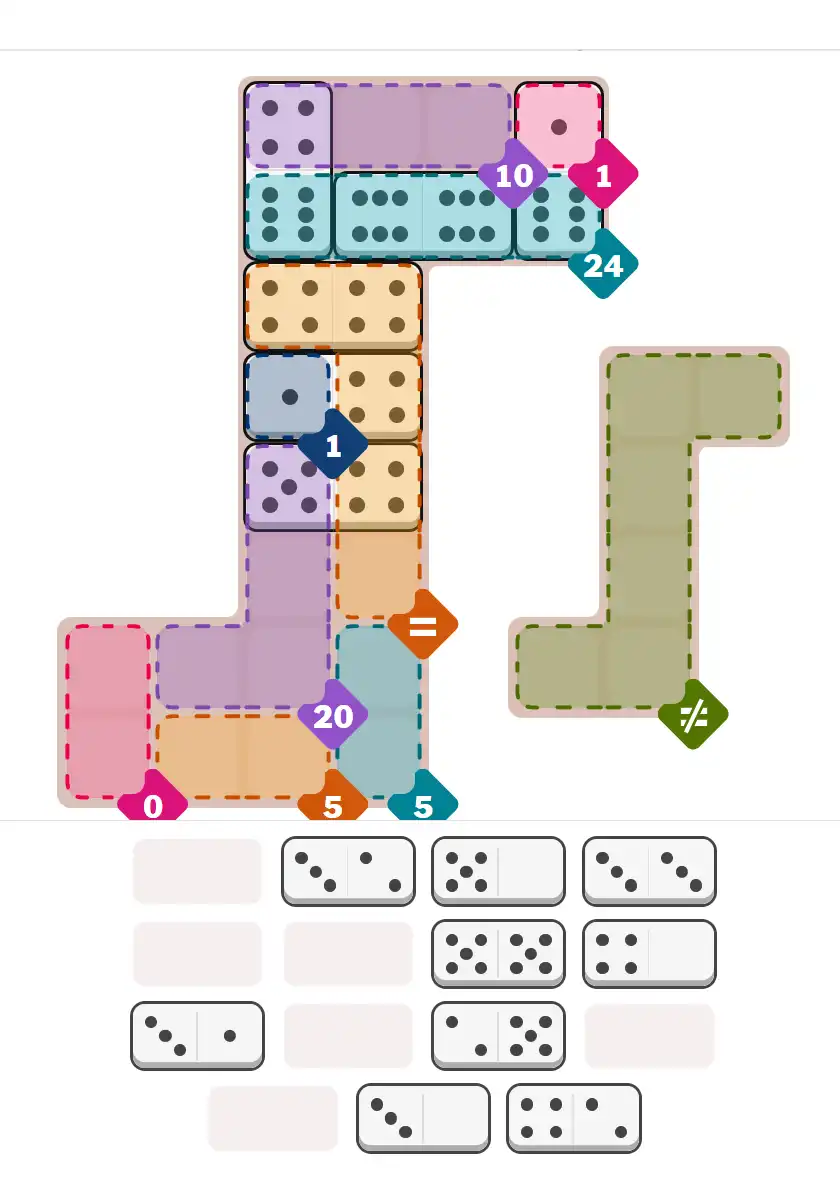
Pips hint for January 16, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

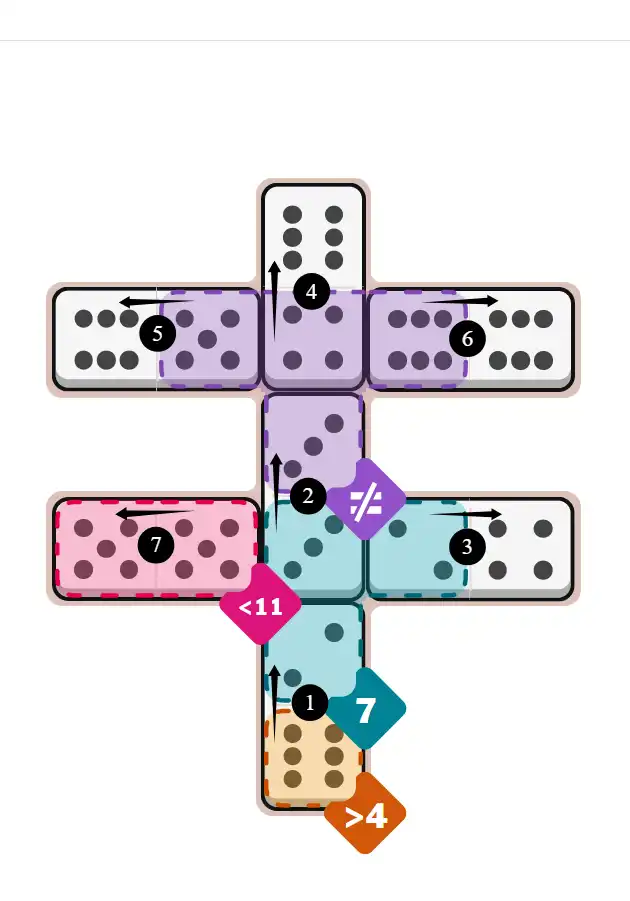
Final Answer: The Solved Grid for Hard Mode

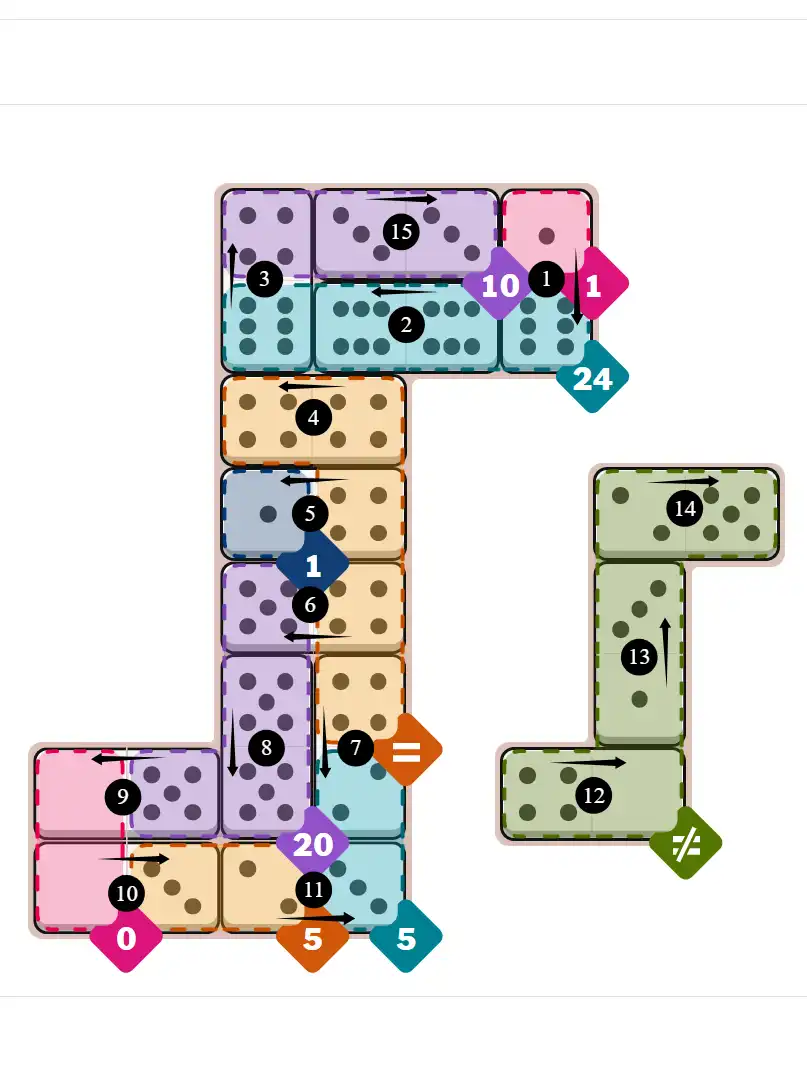
NYT Pips January 16, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-4], [5-0], [4-3], [3-2], [2-2], [0-0].

2

Step 2: Light Blue Equal + Red 3 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. Only 2 dominoes with 3 pips (4-3, 3-2), the domino halves in Light Blue Equal region must be 2. The answer is 2-2, placed vertically; 2-3 (3 into Red 3 region), placed horizontally.

3

Step 3: Purple Equal --(Arrows ③④)

Confirmed by neighboring region and remaining dominoes (6-4, 5-0, 4-3, 0-0). The domino halves in this region must be 0. The answer is 0-0, placed horizontally; 0-5 (5 down into blank), placed vertically.

4

Step 4: Yellow 3 + Blue Equal --(Arrows ⑤⑥)

Confirmed by neighboring region and remaining dominoes (6-4, 4-3). The domino halves in Blue Equal region must be 4. The answer is 3-4 (3 into Yellow 3 region), placed vertically; 4-6 (6 right into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [6-5], [6-4], [6-2], [5-5], [4-2], [3-3]. The domino halves in Light Blue 7 region must come from three different dominoes. The domino halves in Purple Not Equal region must come from four different dominoes. The domino halves in Light Blue 7 region must be 2+2+3, [3-3] must placed in the boundary between Light Blue 7 region and Purple Not Equal region.

2

Step 2: Yellow >4 + Light Blue 7 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Light Blue 7 region must be 2+2+3. Only 2 dominoes with 2 pips (6-2, 4-2), only one domino with 3 pips (3-3). The answer is 6-2 (6 into Yellow >4 region), placed vertically; 3-3 (one 3s into Purple Not Equal region), placed vertically; 2-4 (4 right into blank), placed horizontally.

3

Step 3: Purple Not Equal --(Arrows ④⑤⑥)

Confirmed by neighboring region and remaining dominoes (6-6, 6-5, 6-4, 5-5). The domino halves in this region must be 3+4+5+6 (3s alread come from Arrows ②). The answer is 4-6 (6 up into blank), placed vertically; 5-6 (6 left into blank), placed horizontally; 6-6 (one 6s right into blank), placed horizontally.

4

Step 4: Red <11 --(Arrows ⑦)

The answer is 5-5 (whole domino), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-6], [6-4], [6-1], [5-5], [5-4], [5-2], [5-0], [4-4], [4-2], [4-1], [4-0], [3-3], [3-2], [3-1], [3-0]. Only 4 domino halves that contain 6 pips (6-6, 6-4, 6-1) for Light Blue 24 region. Therefore, the domino halves in Green Not Equal must be 0+1+2+3+4+5. Only 5 domino halves that contain 5 pips (5-5, 5-4, 5-2, 5-0), need four for Purple 20 region, need one for Green Not Equal region.

2

Step 2: Red 1 + Light Blue 24 + Purple 4 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Light Blue 24 region must be 6+6+6+6. The answer is 1-6 (1 into Red 1 region), placed vertically; 6-6, placed horizontally; 6-4 (4 into Purple 10 region), placed vertically.

3

Step 3: Blue 1 + Yellow Equal --(Arrows ④⑤⑥⑦)

Confirmed by neighboring region and step 1 and remaining dominoes. Only one domino left that contain 1 pips (4-1), therefore, the domino halves in Yellow Equal region must be 4. The other dominoes with 4 pips (5-4, 4-4, 4-2, 4-0). The answer is 4-4, placed horizontally; 4-1 (1 into Blue 1 region), placed horizontally; 4-5 (5 into Purple 20 region), placed horizontally; 4-2 (2 into Light Blue 5 region, comfirmed by not more enough 5 pips), placed vertically.

4

Step 4: Purple 20 + Red 0 + Yellow 5 + Light Blue 5 --(Arrows ⑧⑨⑩⑪)

Confirmed by neighboring region and remaining dominoes (5-5, 5-2, 5-0, 4-0, 3-3, 3-2, 3-1, 3-0). The domino halves in Purple 20 region must be 5+5+5+5(one 5s already come from Arrows ⑥). The domino halves in Red 0 region must be 0+0 and come from two different dominoes. The domino halves in Yellow 5 region must be 3+2. The domino halves in Light Blue 5 region must be 3+2 (2s already come from Arrows ⑦). The answer is 5-5, placed vertically; 5-0, placed horizontally; 0-3 (3 into Yellow 5 region), placed horizontally; 2-3 (2 into Yellow 5 region, 3 into Light Blue 5 region), placed horizontally.

5

Step 5: Green Not Equal --(Arrows ⑫⑬⑭)

Confirmed by neighboring region and remaining dominoes (5-2, 4-0, 3-3, 3-1). The domino halves in Green Not Equal region must be 0+1+2+3+4+5. The answer is 4-0, placed horizontally; 5-0, placed horizontally; 1-3, placed vertically; 2-5, placed horizontally.

6

Step 6: Purple 10 --(Arrows ⑮)

Confirmed by neighboring region and remaining dominoes (3-3). 4s alread placed in this region (Arrows ③), need one domino sum to be 6 placed in this region. The answer is 3-3 (whole domino), placed horizontally.

🎥 NYT Pips January 16, 2026 Solution Walkthrough｜Friday Logic Breakdown & Smart Pips Hints

Perfect for solvers who enjoy a methodical, data-driven challenge.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 17, 2026

View Answer →

NYT Pips Hints & Answers for January 15, 2026

View Answer →

NYT Pips Hints & Answers for January 14, 2026

View Answer →

💬 Community Discussion

Leave your comment