NYT Pips Hint, Answer & Solution for January 17, 2026

Jan 17, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

On Saturday, January 17, 2026, NYT Pips rolls into the weekend with a clean, structured logic challenge that’s ideal for focused solvers and careful analysts alike. It’s a Saturday puzzle that rewards patience, making it a great companion for a quiet morning or an afternoon logic break.

Under the editorship of Ian Livengood, today’s puzzle set progresses smoothly from the approachable Easy grid (ID 524) to the more demanding Medium grid (ID 548), before culminating in the tightly constrained Hard grid (ID 570). The difficulty curve feels intentional rather than abrupt, encouraging solvers to build momentum and confidence as they move forward.

Across all three grids, NYT Pips emphasizes disciplined domino management. You’ll need to track sums, inequalities, and equal regions with precision, while constantly reassessing remaining dominoes. This is the kind of puzzle day where a well-timed Pips Hint can save several moves—and where revisiting a pips hint today often reveals why a placement felt forced or inevitable.

With puzzles constructed by Ian Livengood and Rodolfo Kurchan, January 17, 2026 stands out as a data-driven NYT Pips workout. Whether you’re benchmarking your solve speed, studying the logic behind each region, or reviewing a full solution for deeper insight, today’s grids offer a satisfying and methodical test of pure deduction.

Written by Ander

Puzzle Analyst – Nikki

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - Scan for unique sums first

At the start, compare all available domino sums with fixed target regions. If only one domino can hit a specific total, that placement is effectively forced and should be resolved immediately.

💡 Hint #2 - Lock in exact-sum regions early

Exact sum regions like 8 dramatically reduce ambiguity. Once you find a domino that perfectly matches the target, placing it early stabilizes the grid and limits future branching.

💡 Hint #3 - Use orientation constraints to guide placement

When a domino must be placed horizontally or vertically to satisfy two adjacent regions, treat orientation as a key constraint. This often decides not just the domino, but which half belongs in each region.

💡 Hint #4 - Resolve multi-region chains by working backward

For linked regions with <, exact, and sum targets, start from the most restrictive condition. Identify the only viable pip combinations, then cascade placements across neighboring regions to finish efficiently.

💡 Hint #1 - Identify forced high-sum regions

When a region demands a very large total, immediately test whether it can only be satisfied by repeated high pips. Here, the >16 requirement forces the use of all available 6s, sharply narrowing placement options.

💡 Hint #2 - Commit scarce pips early

If only two dominoes contain a critical pip value, their placement becomes unavoidable. Lock them into the demanding region first, and let the remaining half naturally constrain adjacent regions.

💡 Hint #3 - Complete not-equal regions by elimination

For a Not Equal region, list the remaining distinct pips after earlier placements. Once one value is already fixed, the rest of the region often collapses into a single valid combination.

💡 Hint #4 - Use inequality to finish leftovers

Small inequality targets like <4 are ideal cleanup tools. With only a couple of dominoes left, check which half satisfies the limit, then place any unrestricted domino into blank space to close the grid.

💡 Hint #1 - Domino inventory & pip scarcity

Start by counting high-frequency pips. With only six halves showing 6, decide early which sum regions must reserve them. Also note unique values like a single 4-pip domino, as these immediately constrain equals or fixed-sum regions.

💡 Hint #2 - Use unique pips to lock equals regions

When a region requires equal values and only one domino contains a specific pip, that domino becomes forced. Place the unique 4-pip to satisfy the fixed sum, then use the matching pip to resolve the neighboring equal region.

💡 Hint #3 - Resolve exact sums with limited candidates

For a tight target like 10, check which remaining dominoes can pair to reach it. When only two dominoes contain the needed pip, their placement is effectively determined, especially when combined with an inequality constraint.

💡 Hint #4 - Break large sums into forced components

Large totals such as 12 often collapse into obvious combinations once earlier placements remove options. Use pip counts to ensure halves come from different dominoes, then satisfy smaller adjacent sums in the same sweep.

💡 Hint #5 - Chain equal regions to exhaust a pip value

When multiple equal regions appear together, look for a pip value that can fill all of them cleanly. Locking one equal region often cascades into others, and can also free a single-value region like a fixed 6.

💡 Hint #6 - Finish with inequality cleanup

At the end, unequal regions usually resolve themselves. With only two dominoes left, simply ensure the halves differ, then place the remaining identical domino to complete the grid without violating earlier constraints.

🎨 Pips Solver

Jan 17, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

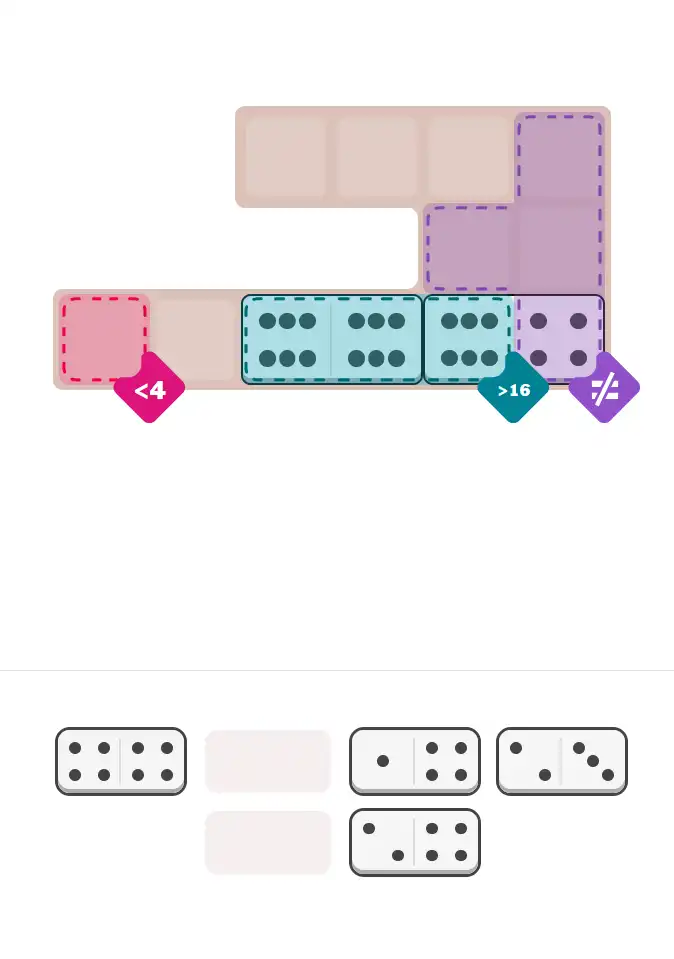
Starting Position & Key First Steps

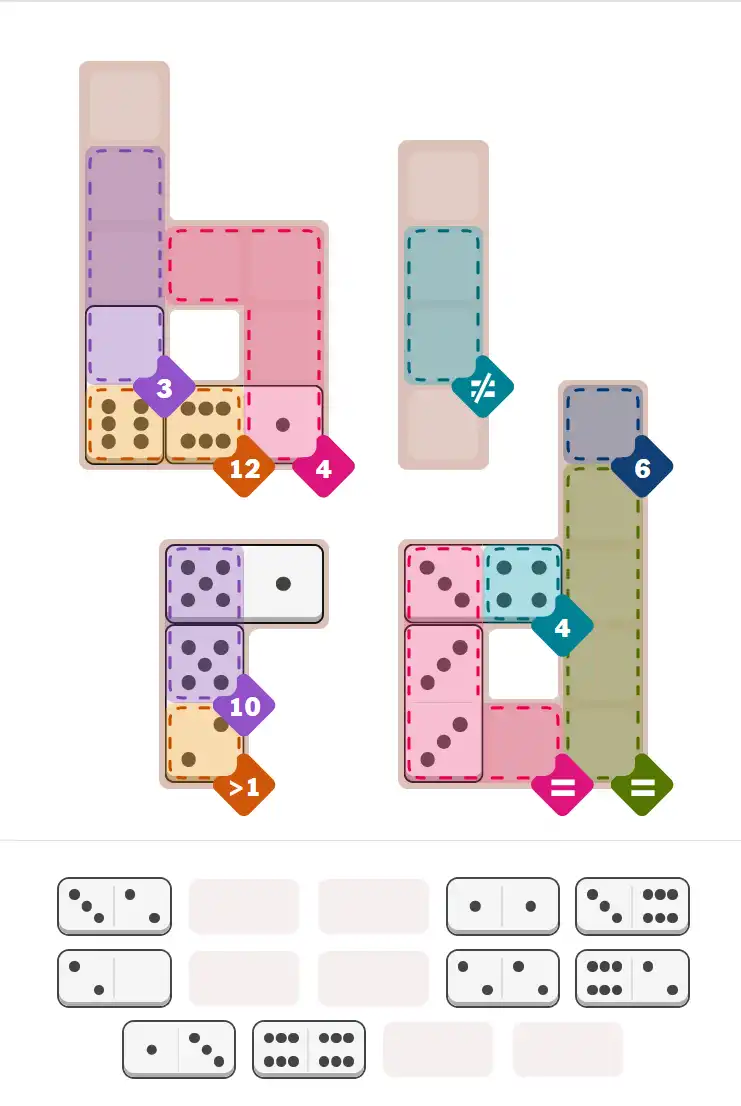
Pips hint for January 17, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

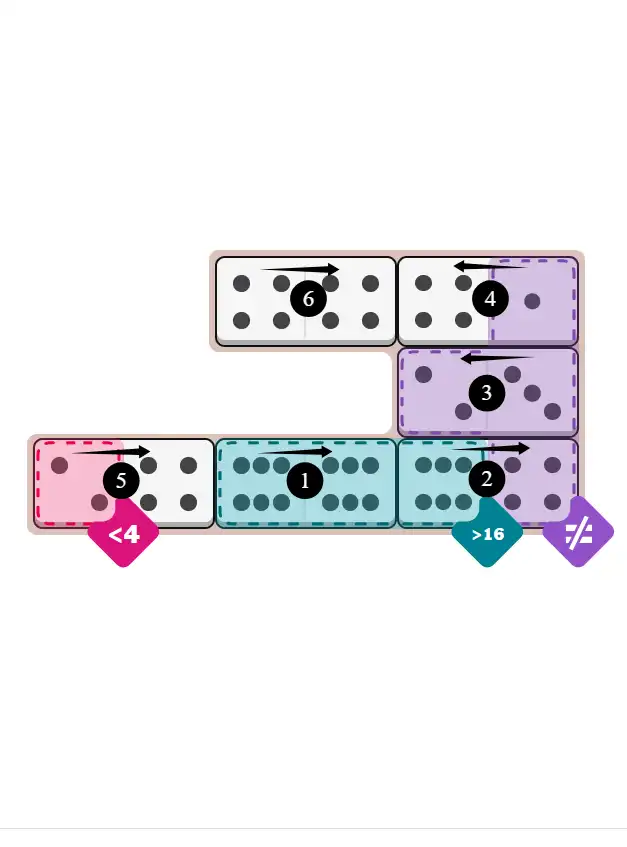
Final Answer: The Solved Grid for Hard Mode

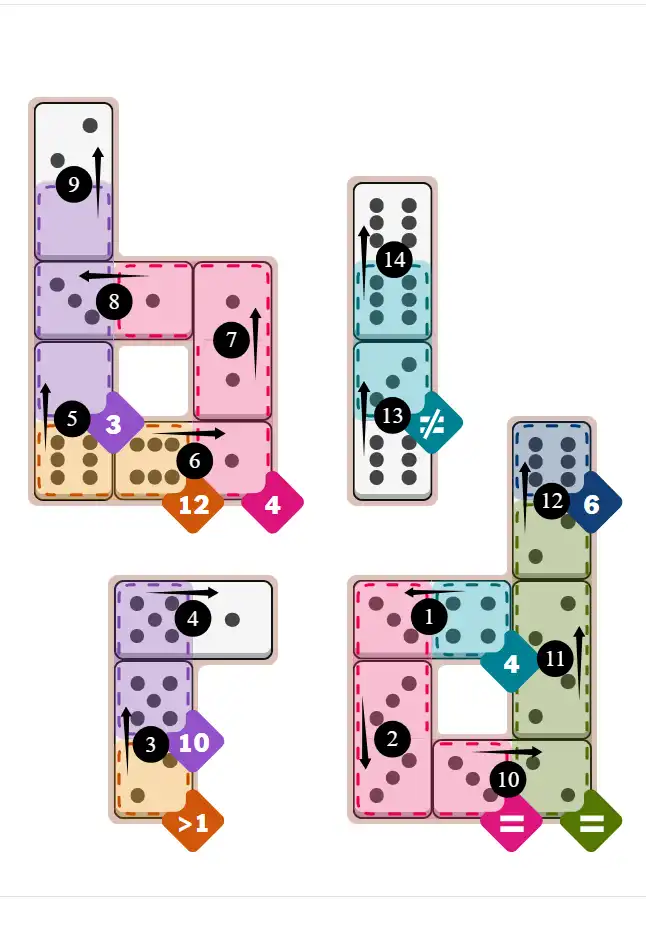
NYT Pips January 17, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-4], [4-4], [4-3], [4-0], [2-1].

2

Step 2: Light Blue 8 --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. Need one domino sum to 8 placed in this region. The answer is 4-4, placed horizontally.

3

Step 3: Blue 4 + Green >2 --(Arrows ②)

Confirmed by neighboring region and relative position and remaining dominoes (6-4, 4-3, 4-0, 2-1). Need one domino placed horizontally in these two regions. The answer is 4-3 (4 into Blue 4 region, 3 into Green >2 region), placed horizontally.

4

Step 4: Purple <3 + Red 7 + Yellow 8 --(Arrows ③④⑤)

Confirmed by neighboring region and remaining dominoes (6-4, 4-0, 2-1). The domino halves in Red 7 region must be 1+6. The domino halves in Yellow 8 region must be 4+4. The answer is 2-1 (2 into Purple <3 region), placed horizontally; 6-4, placed horizontally; 4-0 (0 right into blank), placed horizontally

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [6-4], [4-4], [4-2], [4-1], [3-2]. The domino halves in Light Blue >16 region must be 6+6+6.

2

Step 2: Light Blue >16 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. The domino halves in this region must be 6+6+6, only 2 dominoes with 6 pips (6-6, 6-4). The answer is 6-6, placed horizontally; 6-4 (4 into Purple Not Equal region), placed horizontally.

3

Step 3: Purple Not Equal --(Arrows ③④)

Confirmed by neighboring region and remaining dominoes (4-4, 4-2, 4-1, 3-2). The domino halves in this region must be 4+3+2+1 (4s already come from Arrows ②). The answer is 3-2, placed horizontally; 1-4 (4 left into blank), placed horizontally.

4

Step 4: Red <4 + Top Blank--(Arrows ⑤⑥)

Confirmed by neighboring region and remaining dominoes (4-4, 4-2). The answer is 2-4, placed horizontally (2 into Red <4 region, 4 right into blank); 4-4 (whole domino into Top Blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-6], [6-3], [6-2], [6-1], [6-0], [5-2], [5-1], [4-3], [3-3], [3-2], [3-1], [2-2], [2-0], [1-1]]. Only 6 domino halves that contain 6 pips, need two for Yellow 12 region, need one for Blue 6 region. Only one domino with 4 pips (4-3).

2

Step 2: Light Blue 4 + Red Equal --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 4 pips (4-3), need one domino with the same number placed in Red Equal region. The domino halves in Red Equal region must be 3. The answer is 4-3 (4 into Light Blue 4 region), placed horizontally; 3-3, placed vertically.

3

Step 3: Yellow >1 + Purple 10 --(Arrows ③④)

Confirmed by neighboring region and remaining dominoes. The domino halves in Purple 10 region must be 5+5, only 2 dominoes left that contain 5 pips (5-2, 5-1). The answer is 2-5 (2 into Yellow >1 region), placed vertically; 5-1 (1 right into blank), placed horizontally.

4

Step 4: Yellow 12 + Red 4 + Purple 3 --(Arrows ⑤⑥⑦⑧⑨)

Confirmed by all left regions and remaining dominoes (6-6, 6-3, 6-2, 6-1, 6-0, 3-2, 3-1, 2-2, 2-0, 1-1). The domino halves in Yellow 12 region must be 6+6 and come from two different dominoes. The domino halves in Red 4 region must be 1+1+1+1. Only 3 dominoes left that contain 1 pips (6-1, 3-1, 1-1), the domino halves in Purple 3 region must be 3+0+0. The answer is 6-0, placed vertically; 6-1, placed horizontally; 1-1, placed vertically; 1-3, placed horizontally; 0-2 (2 up into blank), placed vertically.

5

Step 5: Red Equal + Green Equal + Blue 6 --(Arrows ⑩⑪⑫)

Confirmed by neighboring region and remaining dominoes (6-6, 6-3, 6-2, 3-2, 2-2). The domino halves in Green Equal region must be 2. The answer is 3-2 (3 into Red Equal region), placed horizontally; 2-2, placed vertically; 2-6 (6 into Blue 6 region), placed vertically.

6

Step 6: Light Blue Not Equal --(Arrows ⑬⑭)

Confirmed by neighboring region and remaining dominoes (6-6, 6-3). The domino halves in this region must be different. The answer is 6-3 (3 into Light Blue Not Equal region), placed vertically; 6-6 (one 6s into Light Blue Not Equal region), placed vertically.

🎥 NYT Pips January 17, 2026 Solution Walkthrough | Saturday Logic Breakdown & Pips Hints Explained

Perfect for weekend solvers looking to sharpen their logic skills and understand why each move works.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 16, 2026

View Answer →

NYT Pips Hints & Answers for January 15, 2026

View Answer →

NYT Pips Hints & Answers for January 14, 2026

View Answer →

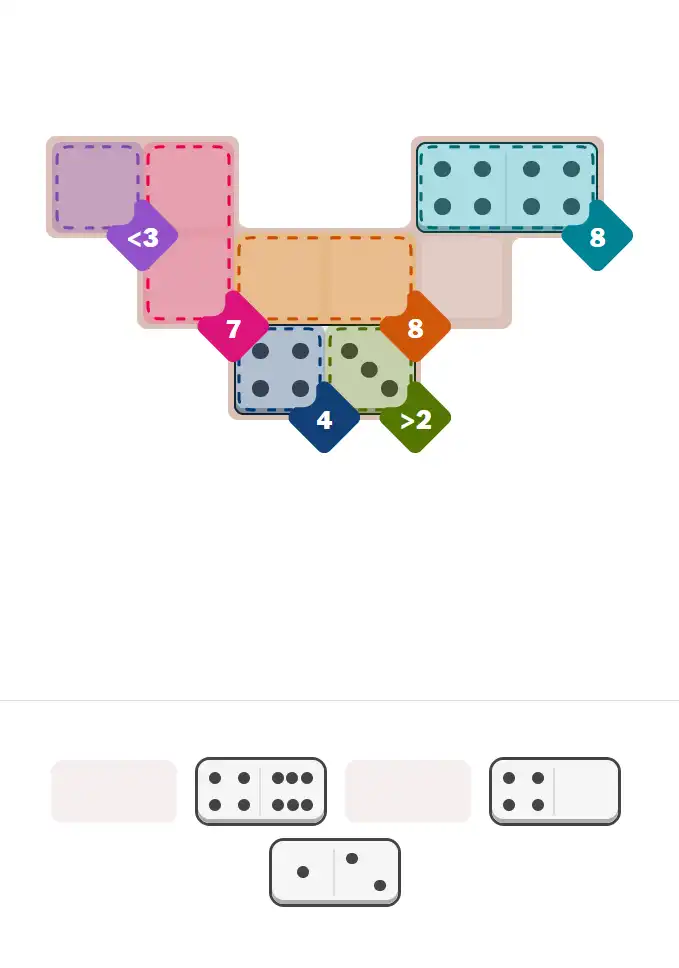
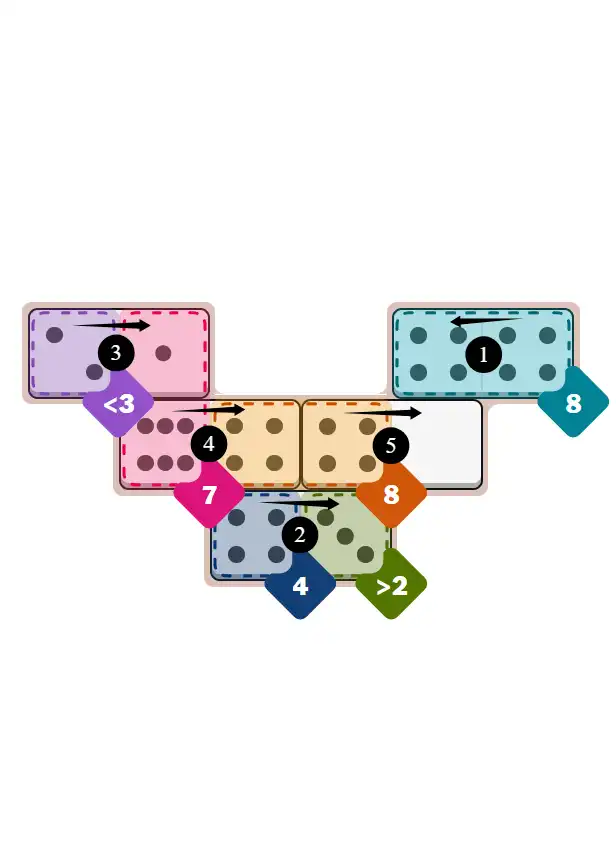
💬 Community Discussion

Leave your comment