NYT Pips Hint, Answer & Solution for November 9, 2025

Nov 9, 2025

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

PIPS HINTS | November 9, 2025 (Sunday) Domino Solutions

PipsNYTHints.com delivers comprehensive pip analysis and hints for today's three-tier challenge.

PUZZLE DATA & HINTS:

→ Easy (ID: 175) | 4 dominoes | Pips hints available at PipsNYTHints.com

→ Medium (ID: 278) | 9 dominoes | 4-pip pattern hints at PipsNYTHints.com

→ Hard (ID: 289) | 12 dominoes | Zero-pip strategy hints at PipsNYTHints.com

DIFFICULTY BREAKDOWN WITH PIPS HINTS:

Easy Puzzle Hints (Constructor: Ian Livengood)

6 constraint regions testing fundamental pip logic. PipsNYTHints.com provides detailed hints for equals spanning three cells and less-than-5 pip conditions. Track domino pips: 2-2, 5-0, 1-0, 4-2.

Medium Puzzle Hints (Constructor: Ian Livengood)

9 dominoes with critical 4-pip resource management. PipsNYTHints.com breaks down the "unequal" constraint requiring different pip values. Expert hints for navigating equals regions and sum constraints. All 4-pip dominoes mapped: 0-4, 1-4, 2-4, 3-4, 4-4, 5-4, 6-4.

Hard Puzzle Hints (Constructor: Rodolfo Kurchan)

12-domino expert grid with 13 constraint regions. PipsNYTHints.com offers strategic hints for sum-0 targets, triple inequalities (<3, <4, >4), and multiple equals zones. Zero-pip inventory: 5-0, 2-0, 0-0 - allocation hints provided.

ACCESS COMPLETE SOLUTIONS:

Visit for:

✓ Step-by-step pip placement hints

✓ Visual pip-counting strategies

✓ Constraint-specific solving hints

✓ Complete domino solutions with pip verification

Test your skills. Get hints when stuck. Master pip logic at PipsNYTHints.com.

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - Key Strategies Used

The Number 1 region (orange) had only ONE possible solution: 0-1. This gave us our entry point.

💡 Hint #1 - Unique Element Identification

Starting with the only domino containing 6 pips gave us a definitive entry point.

💡 Hint #2 - High-Value Sum Strategy

Sum-10 targets point toward double-five or high-pip combinations.

💡 Hint #3 - Flexible Constraint Recognition

The not equal (≠) constraint was intentionally left for last because it's the most permissive.

💡 Hint #1 - The Master Key

Counting how many domino halves contain specific pip values (0, 2, 6) revealed which placements were forced. This technique is ESSENTIAL for expert puzzles.

💡 Hint #2 - Equals Region Cascading

Solving one equals region (orange with 2 pips) limited options for the next equals region (blue with 6 pips), creating a solving chain.

🎨 Pips Solver

Nov 9, 2025

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

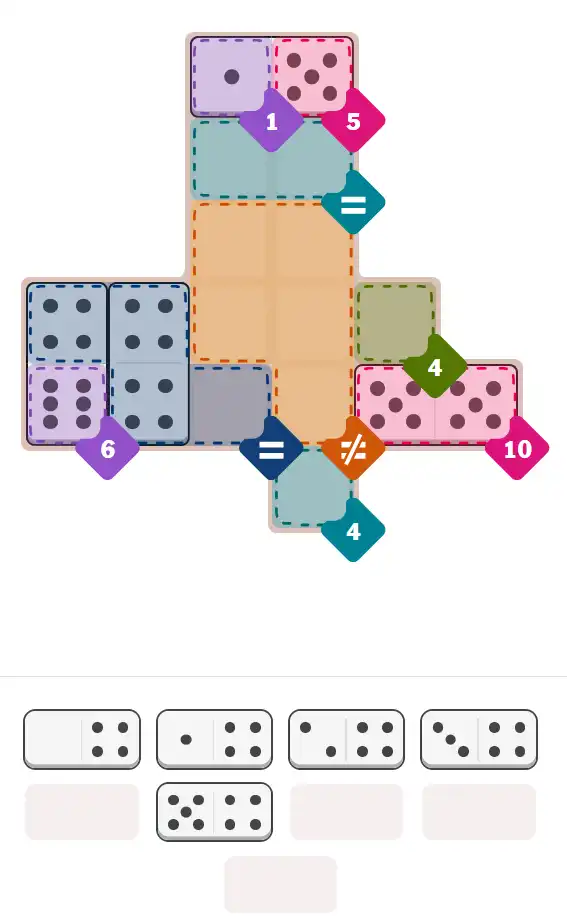
Starting Position & Key First Steps

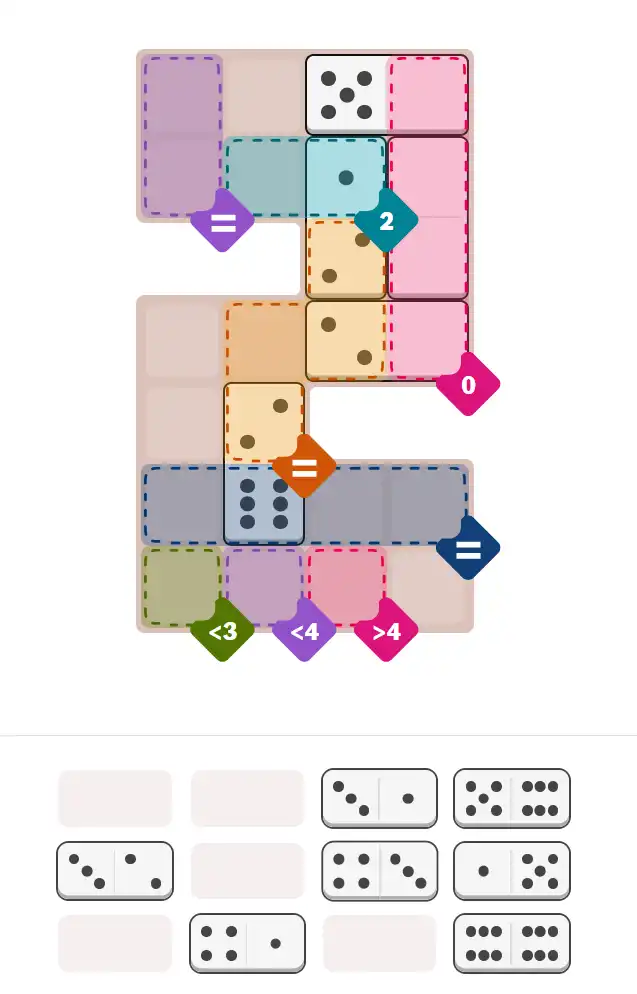
Pips hint for November 9, 2025 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

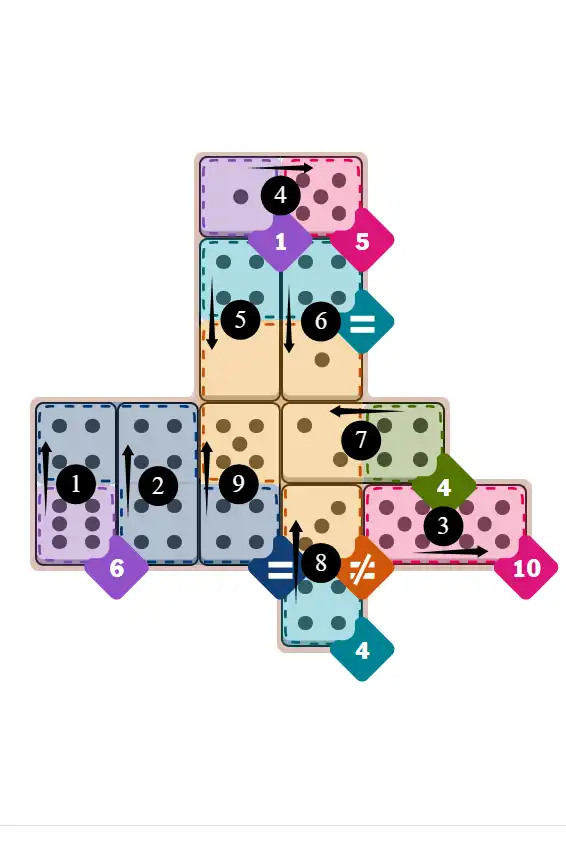
Final Answer: The Solved Grid for Hard Mode

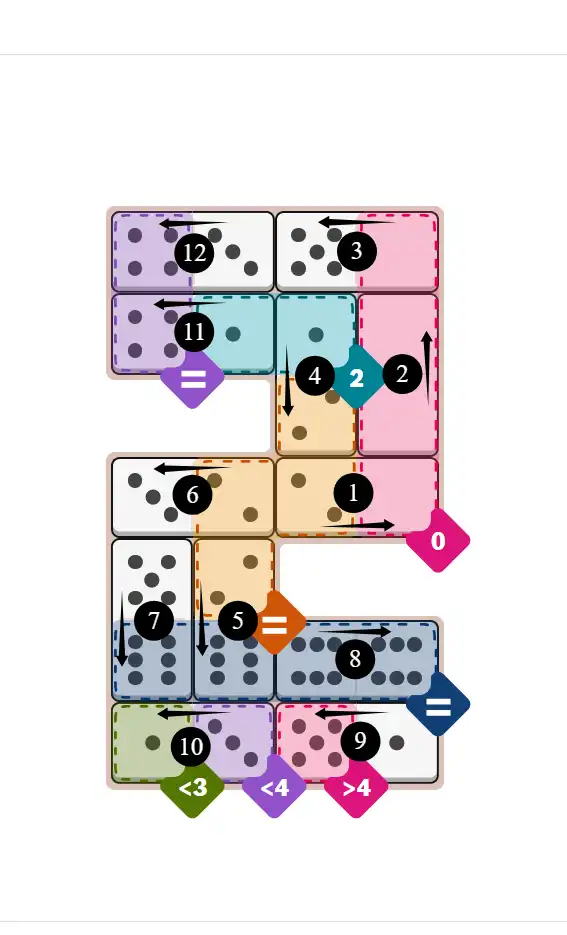
NYT Pips November 9, 2025 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Based on the image, observe the shapes and domino pip counts.

2

Step 2: Number (1)

The answer is 0-1, placed vertically.

3

Step 3: Equal

Confirmed by neighboring area and remaining dominoes. The domino halves in this area must be 2. The answer is 2-4, placed vertically; 2-2, placed vertically.

4

Step 4: Number (5)

The answer is 5-0, placed vertically.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Based on the image, observe the shapes and domino pip counts. There is no single correct answer to this puzzle.

2

Step 2: Number (6)

Only one domino with 6 pips. e.g: The answer is 4-6, placed vertically.

3

Step 3: Blue Equal

Confirmed by step 1 and remaining dominoes. The domino halves in this area must be 4. The answer is 4-4, placed vertically.

4

Step 4: Number (10)

Need one domino sum to 10, confirmed by remaining dominoes. The answer is 5-5, placed horizontally.

5

Step 5: Number (1)

Confirmed by neighboring area and remaining dominoes. There are two choices (1-4 (vertically) or 1-5 (horizontally)). e.g: The answer is 1-5, placed horizontally.

6

Step 6:Not Equal

The domino halves in this space must be different. The remaining dominoes all have 4 pips, and the other halves each have different numbers of pips. Confirmed by neighboring area and remaining dominoes. The answer is 4-0, placed vertically; 4-1, placed vertically; 2-4, placed horizontally; 3-4, placed vertically; 5-4, placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1: Critical Initial Analysis

Looking at all available dominoes, we can count specific pip values: Only 4 domino halves contain 0 pips (for the Number 0 region) Only 4 domino halves contain 2 pips (crucial for equals regions) Only 4 domino halves contain 6 pips (crucial for equals regions) Why this matters: These limited quantities create bottlenecks that determine where specific dominoes MUST go. This is our master key to solving the puzzle! Strategic insight: When certain pip values appear exactly as many times as constraint regions need them, those placements become locked in. This constraint counting technique is essential for expert puzzles.

2

Step 2: Solving the Number 0 Region (Pink, Right Side)

Constraint: The pips in this pink region must sum to 0. Logic chain: Step 1 identified only 4 domino halves with 0 pips The pink 0-region spans multiple domino spaces Looking at neighboring regions and relative positioning We need dominoes that contribute 0 pips to this area Solution: 2-0 domino: Placed horizontally 0-0 domino: Placed vertically (double-zero) 5-0 domino: Placed horizontally Why these placements: These three dominoes provide the necessary 0-pip halves to satisfy the sum-0 constraint. The non-zero halves (2, 5) extend into adjacent regions where they'll help satisfy other constraints. Verification: All cells in pink 0-region contain 0 pips ✓

3

Step 3: Solving the Orange Equal Region (Center)

Constraint: Both domino halves in the orange equal region must be identical. Deduction chain: From Step 1, we know only 4 domino halves contain 2 pips From Step 2, we've already used the 2-0 domino Looking at remaining dominoes with 2 pips and neighboring area requirements The orange equal region connects to the Number 2 (teal) constraint Analysis: The domino halves in this area must be 2. Solution: 1-2 domino: Placed vertically 2-6 domino: Placed vertically 3-2 domino: Placed horizontally Why this works: All orange dashed sections now display 2 pips, satisfying the equals constraint. The other halves (1, 6, 3) extend into adjacent regions, helping build the overall solution. Verification: All orange equal regions show 2 pips ✓

4

Step 4: Solving the Blue Equal Region (Center-Right)

Constraint: Both domino halves in the blue equal region must be identical. Deduction chain: From Step 1, we identified only 4 domino halves with 6 pips From Step 3, we used the 2-6 domino (one 6-pip half) Looking at neighboring areas, relative positioning, and remaining dominoes with 6 pips The blue equal region requires matching high values Analysis: The domino halves in this area must be 6. Solution: 5-6 domino: Placed vertically 6-6 domino: Placed horizontally (double-six) Why this works: Both blue dashed sections now display 6 pips, perfectly satisfying the equals constraint. The 5-pip half from the 5-6 domino extends into adjacent areas. Verification: All blue equal regions show 6 pips ✓

5

Step 5: Solving the Greater-Than 4 Region (Pink, Bottom)

Constraint: The domino half in this space must be MORE than 4 (meaning 5 or 6 pips). Analysis: We've already placed dominoes with 6 pips in previous steps Looking at neighboring constraints and remaining available dominoes We need a high-value pip to satisfy the >4 inequality Solution: 5-1 domino: Placed horizontally Why this works: The 5-pip half satisfies the >4 constraint (5 > 4 ✓). The 1-pip half extends into an adjacent region that can accommodate lower values. Verification: The pink >4 region contains 5 pips ✓

6

Step 6: Solving the Less-Than Regions (Green <3 and Purple <4)

Constraints: Green region: Domino half must be LESS than 3 (so 0, 1, or 2) Purple region: Domino half must be LESS than 4 (so 0, 1, 2, or 3) Combined analysis: These two inequality regions are adjacent, meaning we need a domino that satisfies both constraints simultaneously. Logic: Looking at neighboring areas and remaining available dominoes We need a domino with low pip values on both halves The domino must fit the spatial requirements Solution: 1-3 domino: Placed horizontally Why this works: The 1-pip half falls in the green <3 region (1 < 3 ✓) The 3-pip half falls in the purple <4 region (3 < 4 ✓) Both inequality constraints are satisfied simultaneously! Verification: Green region: 1 < 3 ✓ Purple region: 3 < 4 ✓

7

Step 7: Solving the Purple Equal Region (Top Left)

Constraint: Both domino halves in the purple equal region must be identical. Final placements: With all other constraints satisfied, we can now place the remaining dominoes in the purple equal region. Analysis: Looking at neighboring areas and remaining available dominoes The purple equal region requires matching pip values Examining what's left in our domino inventory Solution: 4-1 domino: Placed horizontally 4-3 domino: Placed horizontally Why this works: The purple equal region shows matching pip values (likely 4s based on the dominoes used), satisfying the equals constraint. The other halves (1 and 3) fit logically with adjacent regions. Verification: All purple equal sections show matching pips ✓

🎥 Watch today's full walkthrough video for Easy, Medium, and Hard puzzles.

This video covers step-by-step solutions for all difficulty levels (Easy, Medium, Hard) and highlights key strategies for each. Watch it alongside the step-by-step walkthrough above for best results.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for November 12, 2025

View Answer →

NYT Pips Hints & Answers for November 11, 2025

View Answer →

NYT Pips Hints & Answers for November 10, 2025

View Answer →

💬 Community Discussion

Leave your comment