NYT Pips Hint, Answer & Solution for December 29, 2025

Dec 29, 2025

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Join the community challenge for the Daily Domino Puzzle on Monday, December 29, 2025, a perfect way to unwind during the year-end season and keep your mind sharp before the new year begins.

Today’s puzzle welcomes all skill levels, guiding you through easy, medium, and hard grids that steadily build in complexity. Each grid is packed with classic domino logic, clever constraints, and satisfying deductions that reward careful observation of pips, sums, and placements. If you’re looking for a helpful pips hint today, paying attention to how values interact across regions can unlock progress faster than expected.

This is more than just a puzzle — it’s a shared experience.

Compare strategies with the community, exchange hints, and enjoy that unmistakable “aha” moment when the solution finally falls into place. Whether you solve solo or alongside others, today’s challenge is designed to spark discussion and discovery.

Edited by Ian Livengood, with puzzles crafted by Ian Livengood (easy) and Rodolfo Kurchan (medium and hard), this Daily Domino Puzzle blends thoughtful design with approachable logic. It’s an ideal moment to slow down, reflect on your puzzle-solving journey this year, and enjoy the simple joy of connecting dots — and domino pips — together.

Written by Joe

Puzzle Analyst – Sophia

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - A piece of cake

Try.

💡 Hint #1 - High-Pip Scarcity Scan

Begin by counting how often high pips appear across all dominoes. With only three 6s, three 5s, and three 4s available, five different 10-sum regions cannot all use the same values. Early awareness of pip scarcity prevents impossible combinations later.

💡 Hint #2 - Forced Decomposition of 10

When a sum region cannot be built from the most obvious high pairs, break the target into uncommon combinations. Here, 10 must be formed as 5+2+3, forcing the use of the only available 2 and 3 pips and fixing domino orientation immediately.

💡 Hint #3 - Parallel Sum Locking

Multiple regions sharing the same target often collapse into identical pip pairs. After removing smaller values, the remaining 10-sum regions are forced into 4+6. Lock these in together to eliminate ambiguity and accelerate the solve.

💡 Hint #4 - Threshold-Guided Placement

When a sum region touches a greater-than constraint, assign the minimum valid pip to satisfy the inequality. This allows the remaining high pips to complete the sum cleanly while preserving flexibility in adjacent blank cells.

💡 Hint #1 - Pips Availability Check

Start by counting high-value pips. There are only five domino halves with 6 pips, and specific sum regions already demand all of them. When pips are scarce, lock them into required regions first. This immediately forces the Yellow 20 region to be composed entirely of 5s.

💡 Hint #2 - Forced Sums with Maximum Pips

When a sum target cannot be achieved by mixed values, identical high pips become mandatory. No domino can sum to 12 naturally, so Blue 12 must be 6+6. Use this forced placement to confirm orientations and push remaining high pips into fixed regions.

💡 Hint #3 - Equal Regions Reveal Exact Pips

Equal regions are powerful filters. Once higher pips are allocated elsewhere, equal constraints often collapse to a single value. Here, Yellow Equal must be 3s, which cascades into precise assignments for the neighboring Red 3 and Green >3 regions.

💡 Hint #4 - Low Target Meets Equality

When a small sum region touches an equal region, think in pairs. Purple Equal can only be 2s, leaving 3 as the only valid partner for the Top Red 3 region. Use minimal pips to satisfy tight constraints cleanly.

💡 Hint #5 - Not Equal Means Mixed Values

Not Equal regions reject doubles and uniform pips. Once remaining dominoes are limited, look for whole dominoes whose halves differ naturally. This avoids accidental equality and preserves flexibility in surrounding regions.

💡 Hint #6 - Distribute Remaining Pips Intentionally

At this stage, track leftover pips carefully. Not Equal regions often require a full spread of values rather than a sum. Assign dominoes so that high pips serve mandatory sum regions, while lower pips absorb inequality constraints.

💡 Hint #7 - Final Fit with Threshold Regions

Threshold regions like <3 or >3 are best solved last. Once all other pips are placed, the remaining domino often fits uniquely. Use the final high pip to complete the required sum and slide the low pip into the strict threshold region.

🎨 Pips Solver

Dec 29, 2025

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

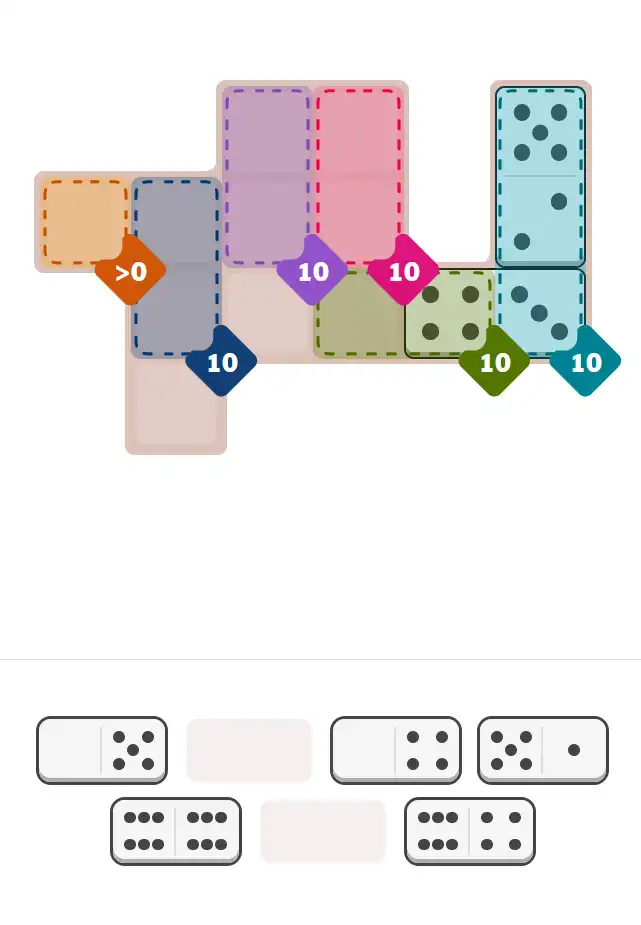
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

Starting Position & Key First Steps

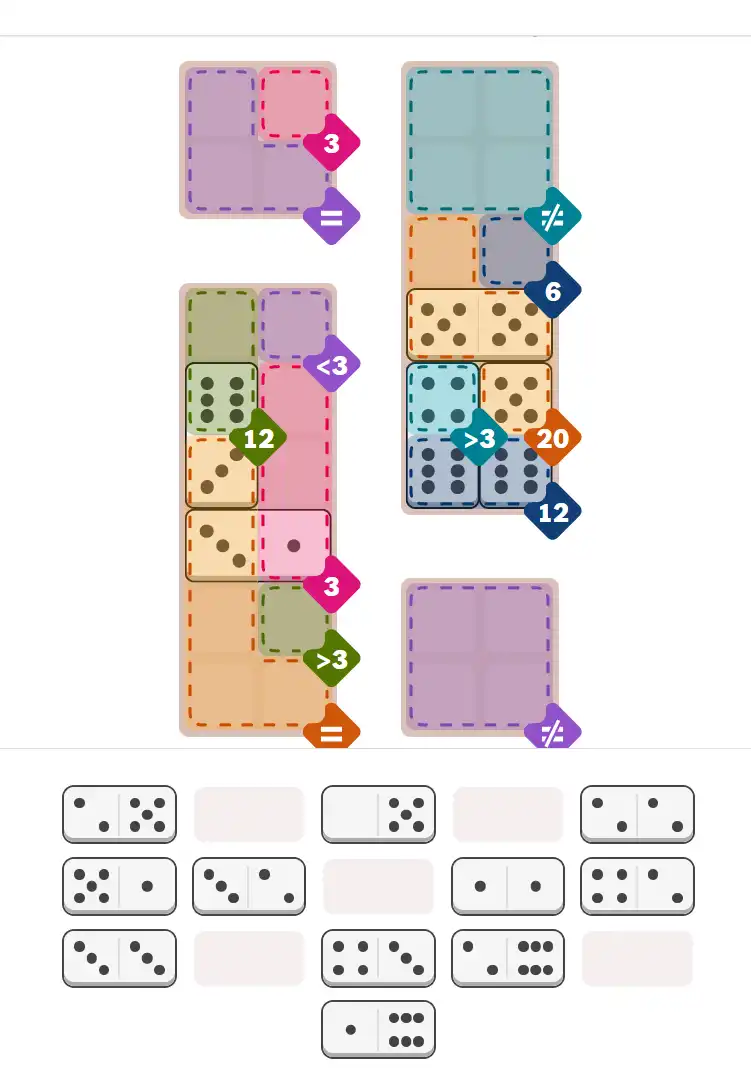
Pips hint for December 29, 2025 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

Final Answer: The Solved Grid for Hard Mode

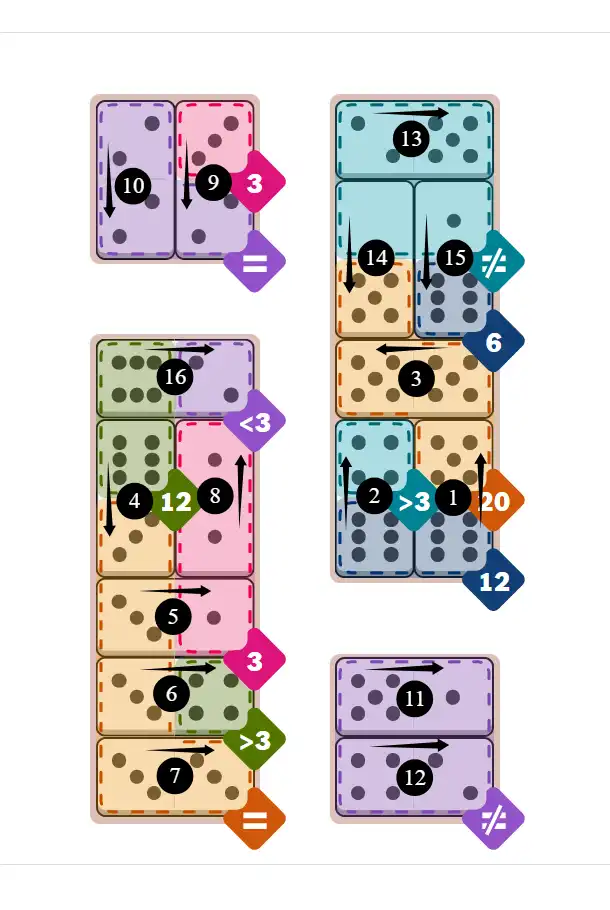
NYT Pips December 29, 2025 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-4], [5-5], [4-4], [4-2], [4-1].

2

Step 2: Yellow 8+ Light Blue 1 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. Need one domino sum to 8 placed in Yellow 8 region. The answer is 4-4, placed horizontally; 1-4 (1 into Light Blue 1 region, 4 up into blank), placed vertically.

3

Step 3: Green Equal --(Arrows ③)

Confirmed by neighboring region and remaining dominoes (6-4, 5-5, 4-2). Need one domino with the same number placed in this region. The answer is 5-5 (whole domino), placed horizontally.

4

Step 4: Red Equal + Purple >5 + Blue <3 --(Arrows ④⑤)

Confirmed by neighboring region and remaining dominoes (6-4, 4-2). The domino halves in Red Equal region must be 4. The answer is 4-6 (6 into Purple >15 region), placed horizontally; 4-2 (2 into Blue <3 region), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [6-4], [5-2], [5-1], [5-0], [4-3], [4-0]. There are five Number 10 regions. Only 3 domino halves that contain 6 pips and 3 domino halves that contain 4 pips. Only 3 domino halves that contain 5 pips.

2

Step 2: Light Blue 10 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. The domino halves in this region must be 5+2+3. Only 2 dominoes with 2 pips and 3 pips. The answer is 5-2 (whole domino), placed vertically; 3-4 (4 into Green 10 region), placed horizontally.

3

Step 3: Green 10 + Red 10 + Purple 10 --(Arrows ③④⑤)

Confirmed by neighboring region and step 2 and remaining dominoes (6-6, 6-4, 5-1, 5-0, 4-0). The domino halves in these three regions must be 4+6. The answer is 6-6, placed vertically; 4-6, placed horizontally; 4-0 (0 down into blank), placed vertically.

4

Step 4: Blue 10 + Yellow >0 --(Arrows ⑥⑦)

Confirmed by neighboring region and remaining dominoes (5-1, 5-0). The domino halves in Blue 10 region must be 5+5. The answer is 5-1 (1 into Yellow >0 region), placed horizontally; 5-0 (0 down into blank), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-5], [6-4], [6-3], [6-2], [6-1], [5-5], [5-2], [5-1], [5-0], [4-3], [4-2], [3-3], [3-2], [3-1], [2-2], [1-1]. Only 5 domino halves that contain 6 pips, need two for Green 12 region and two for Blue 12 region, need one for Blue 6 region. Therefore, the domino halves in Yellow 20 region must be 5+5+5+5.

2

Step 2: Blue 12 + Light Blue >3 + Yellow 20 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. No domino sum to 12. The domino halves in Blue 12 must be 6+6. The domino halves in Yellow 20 must be 5+5+5+5. The answer is 6-5, placed vertically; 6-4 (4 into Light Blue >3 region), placed vertically; 5-5 (whole domino), placed horizontally.

3

Step 3: Yellow Equal + Middle Red 3 + Green >3 --(Arrows ④⑤⑥⑦⑧)

Confirmed by neighboring region and remaining dominoes. The domino halves in Yellow Equal region must be 3. The domino halves in Middle Red 3 region must be 1+1+1. The answer is 6-3 (6 into Green 12 region), placed vertically; 3-1, placed horizontally; 3-4 (4 into Green >3 region), placed horizontally; 3-3, placed horizontally; 1-1, placed vertically.

4

Step 4: Top Red 3 + Purple Equal --(Arrows ⑨⑩)

Confirmed by neighboring region and remaining dominoes. The domino halves in Purple Equal region must be 2. The answer is 3-2 (3 into Top Red 3 region), placed vertically; 2-2, placed vertically.

5

Step 5: Purple Not Equal --(Arrows ⑪⑫)

Confirmed by left regions and remaining dominoes (6-2, 6-1, 5-2, 5-1, 5-0, 4-2). The domino halves in this region must be different. Need two whole dominoes placed in this region. The answer is 5-1 (whole domino), placed horizontally; 4-2 (whole domino), placed horizontally.

6

Step 6: Light Blue Not Equal + Blue 6--(Arrows ⑬⑭⑮)

Confirmed by left regions and remaining dominoes (6-2, 6-1, 5-2, 5-0). The domino halves in Light Blue Not Equal region must be 5+2+0+1. The answer is 2-5 (whole domino), placed horizontally; 0-5 (5 into Yellow 20 region), placed vertically; 1-6 (6 into Blue 6 region), placed vertically.

7

Step 7: Green 12 + Purple <3--(Arrows ⑯)

The answer is 6-2 (6 into Green 12 region, 2 into Purple <3 region), placed horizontally.

🎥 Easy to Hard Logic Breakdown & Pips Strategy Explained

If you’re looking for a practical pips hint today, this is a great example of how small numerical clues guide the entire grid

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for December 28, 2025

View Answer →

NYT Pips Hints & Answers for December 27, 2025

View Answer →

NYT Pips Hints & Answers for December 26, 2025

View Answer →

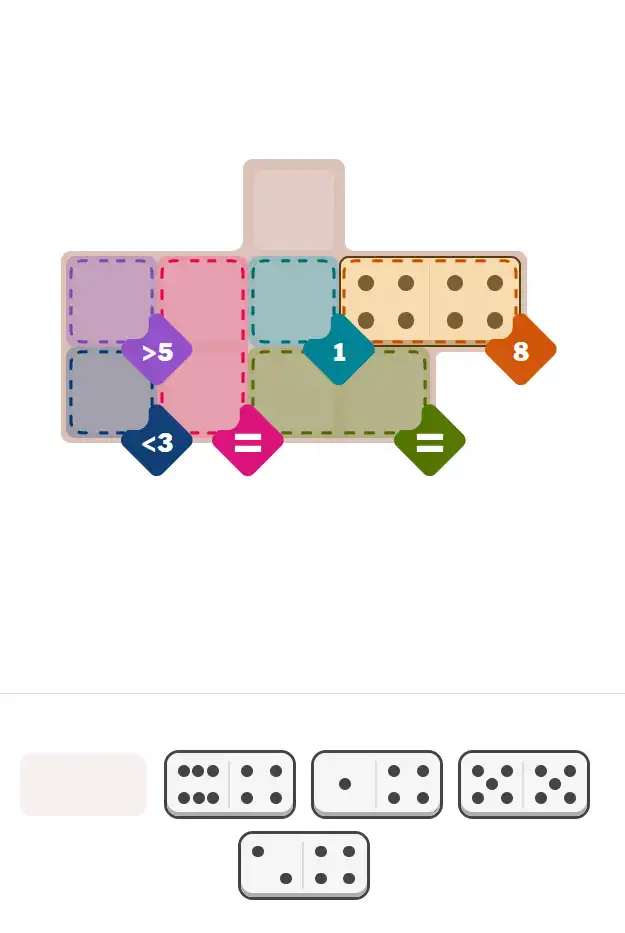
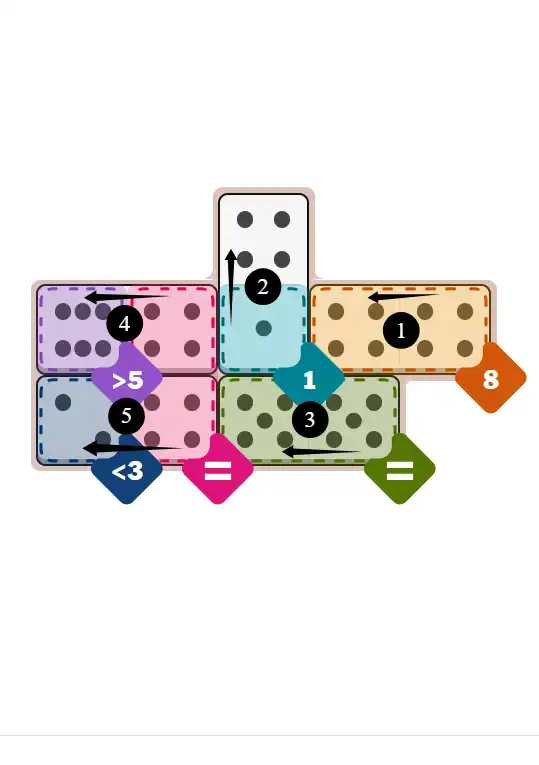
💬 Community Discussion

Leave your comment