NYT Pips Hint, Answer & Solution for February 1, 2026

Feb 1, 2026

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

On Sunday, February 1, 2026, NYT Pips rolls out a thoughtfully structured three-puzzle set built to genuinely test your logic, focus, and domino-tracking skills. It’s a perfect weekend puzzle session—challenging enough to feel rewarding, but paced so you can settle in and think things through.

Edited by Ian Livengood, today’s progression feels intentional: each puzzle gently raises the bar, guiding solvers from clean early deductions to deeper, more demanding logic chains.

The easy puzzle (ID 600) opens with a compact grid and a restrained domino set. This is where careful observation pays off—spotting basic sums, equals regions, and early eliminations gives you quick momentum and confidence. It’s an ideal place to warm up or share a quick Pips hint today with other players.

The medium puzzle (ID 620), designed by Rodolfo Kurchan, shifts gears with uneven regions and layered constraints. Here, success depends on disciplined domino management and constant cross-checking. Many solvers will find this puzzle rewarding to pause, reassess, and compare alternative solution paths.

The hard puzzle (ID 646) delivers the real endurance test. With a larger layout, multiple “less than” regions, and high-value domino interactions, it rewards patience and precision. Each correct placement tightens the grid, making this puzzle especially satisfying for solvers who enjoy long logic chains and structured deduction.

Whether you’re tracking personal performance, refining advanced strategies, or searching for reliable Pips hints and solutions dated February 1, 2026, this Sunday NYT Pips set offers a clear benchmark for real progress—and plenty to analyze, discuss, and learn from.

Written by Joe

Puzzle Analyst – Sophia

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - Observe

Only 2 domino halves that contain 6 pips (6-4, 6-0) for Blue 6 region and Yellow 6 region.

💡 Hint #1 - Scan for Unique Pip Values

Begin by checking whether any region depends on a pip value that appears only once across all dominoes. When a pip is unique, the domino containing it becomes a forced candidate, even before considering exact placement.

💡 Hint #2 - Anchor Fixed-Sum Regions Early

Regions with an exact sum and a single feasible domino should be resolved immediately. Locking these anchors reduces uncertainty and constrains neighboring regions without needing trial placements.

💡 Hint #3 - Fill Unequal Regions with Coverage Logic

For Not Equal regions, focus on covering all required pip values rather than exact positions. Identify which domino is necessary to supply a missing value set, then let that choice cascade into nearby sum or limit regions.

💡 Hint #4 - Resolve Equals Using Remaining Doubles

Once most options are eliminated, equal regions often collapse to the only remaining double. Use this to finalize surrounding greater-than regions and safely place any leftover high-value dominoes.

💡 Hint #1 - Global Count Before Placement

Start by counting scarce pip values across all dominoes. When multiple regions require low totals or strict upper limits, identify which pip numbers are limited and reserve them early. This kind of global inventory check often forces at least one region’s composition before any placement happens.

💡 Hint #2 - Lock High Sums First

Large sum regions are best resolved as early anchors. If only one domino can realistically satisfy a high target, place it immediately. This stabilizes the grid and sharply narrows options for adjacent low or less-than regions.

💡 Hint #3 - Use Extremes to Resolve Equals

Equal regions become solvable when extreme values (like zeros or doubles) are scarce. Track where those extremes must go, then back-solve the remaining equal totals. This often resolves multiple regions at once without guessing.

💡 Hint #4 - Stack Constraints Across Neighboring Regions

When several adjacent regions all have upper limits, solve them together instead of one by one. Assign the smallest possible values first, then confirm that remaining larger values still fit nearby constraints.

💡 Hint #5 - Finish by Elimination, Not Calculation

In the final stage, avoid recalculating sums. Instead, look at the remaining dominoes and match them to the only regions they can legally fit. Endgame Pips solving is about exclusion and inevitability, not arithmetic.

🎨 Pips Solver

Feb 1, 2026

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

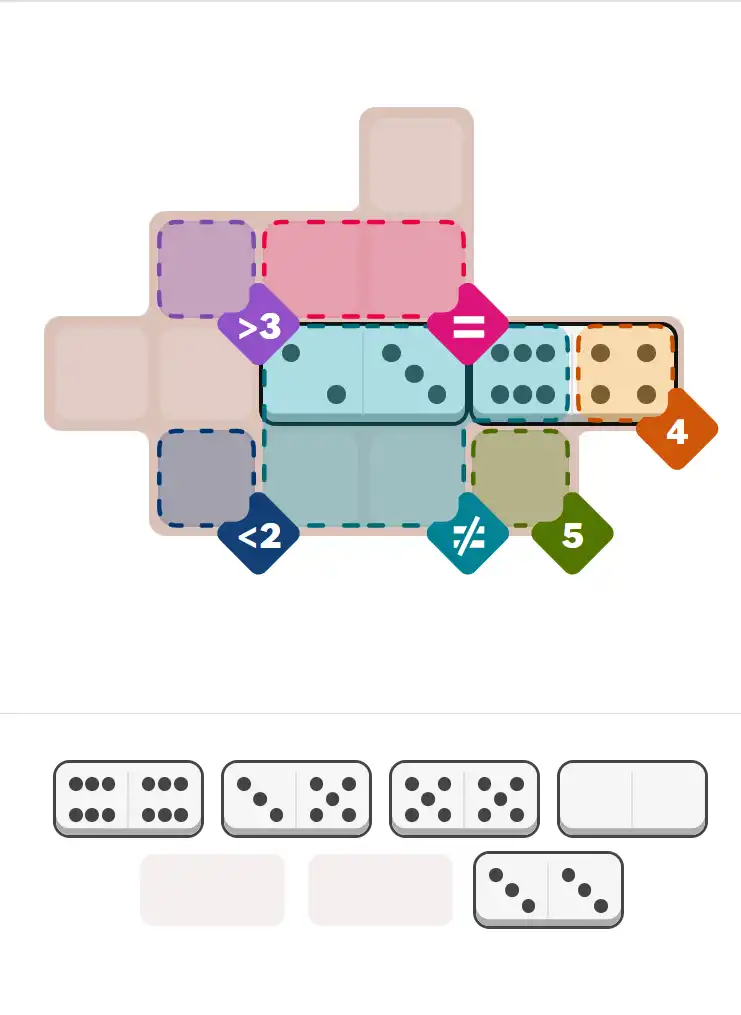
Starting Position & Key First Steps

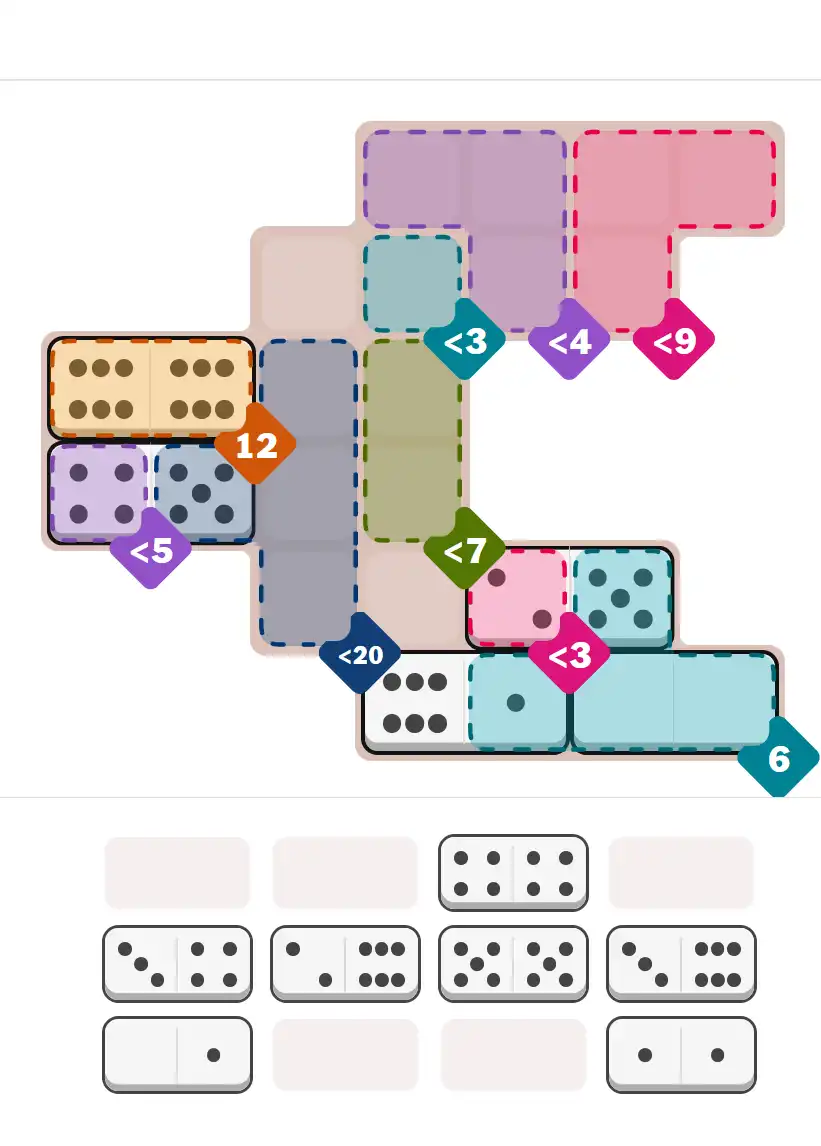
Pips hint for February 1, 2026 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

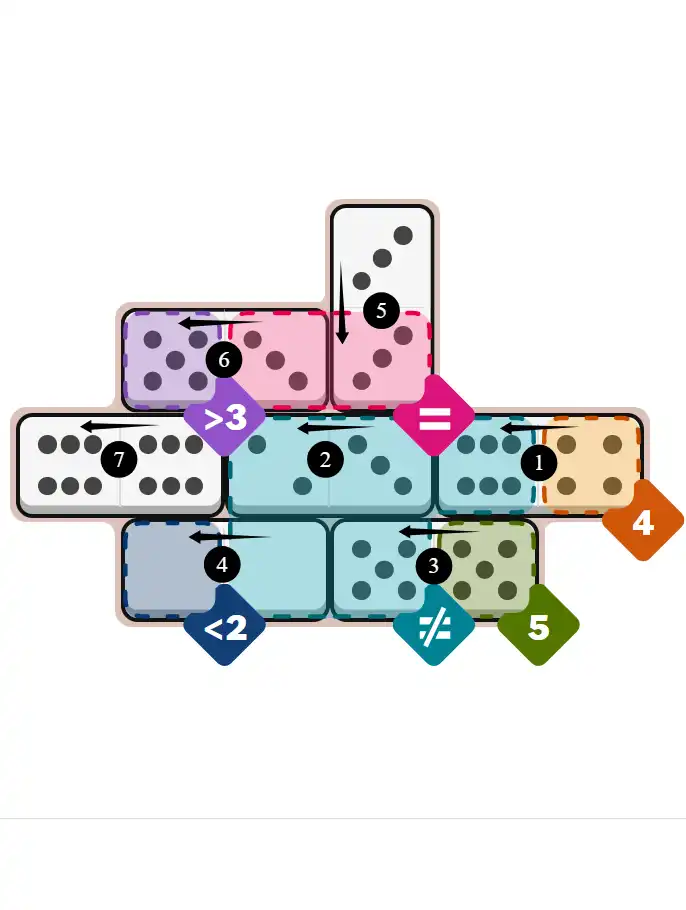
Final Answer: The Solved Grid for Hard Mode

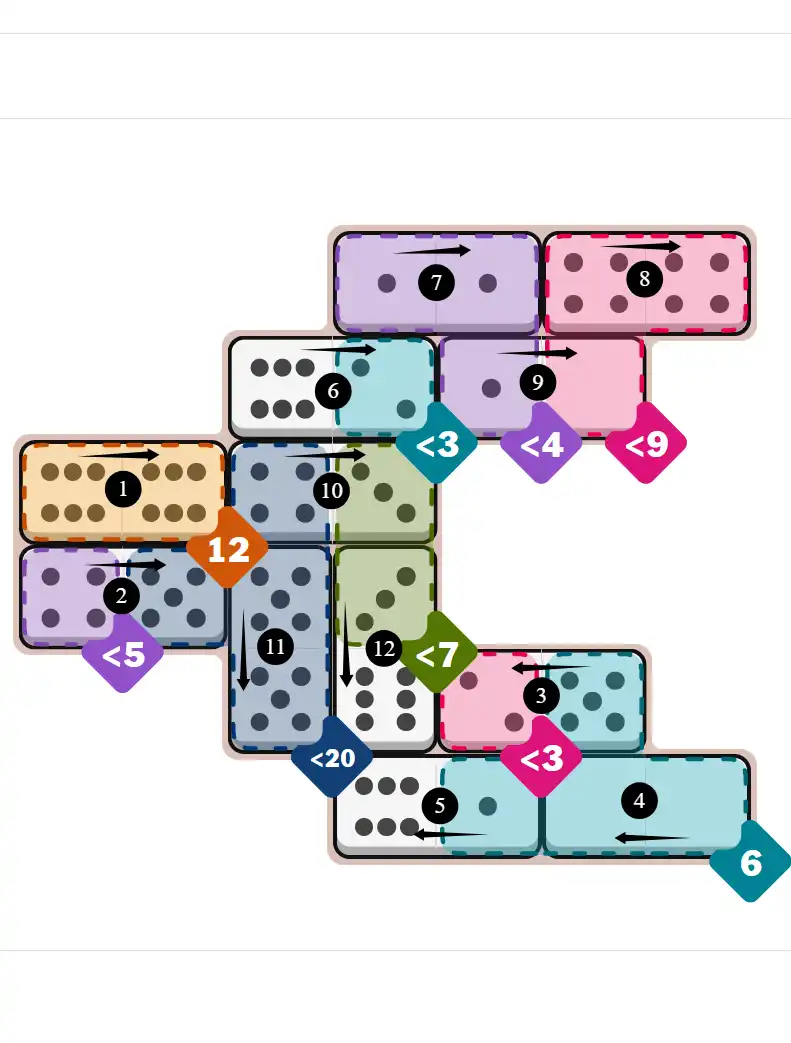
NYT Pips February 1, 2026 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-4], [6-0], [5-0], [4-0], [3-3]. Only 2 dominoes with 6 pips (6-4, 6-0) for Blue 6 region and Yellow 6 region.

2

Step 2: Blue 6 + Purple Equal + Green Equal + Yellow 6 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. The domino halves in Purple Equal region and Green Equal region must be 0 or 4. e.g: The domino halves in Purple Equal must be 0, then the domino halves in Green Equal must be 4. The answer is 6-0 (6 into Blue 6 region), placed vertically; 0-4, placed horizontally; 4-6 (6 into Yellow 6 region), placed vertically.

3

Step 3: Light Blue Equal --(Arrows ④)

Confirmed by neighboring region and remaining dominoes (5-0, 3-3). The answer is 3-3 (whole domino into Light Blue Equal), placed horizontally.

4

Step 4: Red >4 + Purple 0 --(Arrows ⑤)

The answer is 5-0 (5 into Red >4 region, 0 into Purple 0 region), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [6-4], [5-5], [5-3], [3-3], [3-2], [0-0]. Only one domino half that contain 4 pips for Yellow 4 region.

2

Step 2: Yellow 4 --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 4 pips (6-4). The answer is 4-6 (4 into Yellow 4 region, 6 into Light Blue Not Equal region), placed horizontally.

3

Step 3: Light Blue Not Equal + Green 5 + Blue <2 --(Arrows ②③④)

Confirmed by neighboring region and relative position and remaining dominoes (6-6, 5-5, 5-3, 3-3, 3-2, 0-0). The domino halves in Light Blue Not Equal region must be 0+2+3+5+6 (6s already come from Arrows ①), therefor, [3-2] must placed in Light Blue Not Equal region. The answer is 3-2 (whole domino), placed horizontally; 5-5 (one 5s into Green 5 region), placed horizontally; 0-0 (one 0s into Blue <2 region), placed horizontally.

4

Step 4: Red Equal + Purple >3 + Left Blank --(Arrows ⑤⑥⑦)

Confirmed by neighboring region and remaining dominoes (6-6, 5-3, 3-3). The domino halves in Red Equal must be 3. The answer is 3-3 (one 3s up into blank), placed vertically; 3-5 (5 into Purple >3 region), placed horizontally; 6-6 (whole domino into Left Blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-6], [6-3], [6-2], [6-1], [5-5], [5-4], [5-2], [4-4], [4-3], [1-1], [1-0], [0-0]. Only 6 dominoes that contain less than 3 pips (6-2, 6-1, 5-2, 1-1, 1-0, 0-0), need one for Light Blue <3 region, need one for Red <3 region, need two for Purple <4 region, need two for Light Blue 6 region. Only 2 domino halves left that contain 3 pips (6-3, 4-3), therefore, the domino halves in Green <7 region must be 3+3.

2

Step 2: Yellow 12 + Purple <5 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. [6-6] must placed in Yellow 12 region. The answer is 6-6, placed horizontally; 4-5 (4 into Purple <5 region), placed horizontally.

3

Step 3: Red <3 + Light Blue Equal --(Arrows ③④⑤)

Confirmed by all left regions and relative position and remaining dominoes. Only 2 dominoes with 0 pips (1-0, 0-0), [0-0] must placed in Light Blue Equal region. Therefore, the domino halves in Light Blue Equal region must be 5+0+0+1. The answer is 5-2 (2 into Red <3 region), placed horizontally; 0-0, placed horizontally; 1-6 (6 left into blank), placed horizontally.

4

Step 4: Light Blue <3 + Purple <4 + Red <9 --(Arrows ⑥⑦⑧⑨)

Confirmed by neighboring region and remaining dominoes (6-3, 6-2, 5-5, 4-4, 4-3, 1-1, 1-0). The domino half in Light Blue <3 must be 2. The domino halves in Purple <4 region must be 1+1+1. The domino halves in Red <9 region must be 0+4+4. The answer is 6-2 (6 into blank), placed horizontally; 1-1, placed horizontally; 1-0, placed horizontally; 4-4, placed horizontally.

5

Step 5: Blue <20 + Green <7 --(Arrows ⑩⑪⑫)

Confirmed by neighboring region and remaining dominoes (6-3, 5-5, 4-3). The domino halves in Blue <20 region must be 5+5+5+4 (one 5s already come from Arrows ②). The domino halves in Green <7 region must be 3+3. The answer is 4-3, placed horizontally; 5-5, placed vertically; 3-6 (6 down into blank), placed vertically.

🎥 NYT Pips Solution Walkthrough – Sunday, February 1, 2026 | Easy to Hard Logic Breakdown & Pips Hints Today

Perfect for weekend solvers who enjoy slowing down, analyzing each move, and turning every puzzle into a learning opportunity.

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for January 31, 2026

View Answer →

NYT Pips Hints & Answers for January 30, 2026

View Answer →

NYT Pips Hints & Answers for January 29, 2026

View Answer →

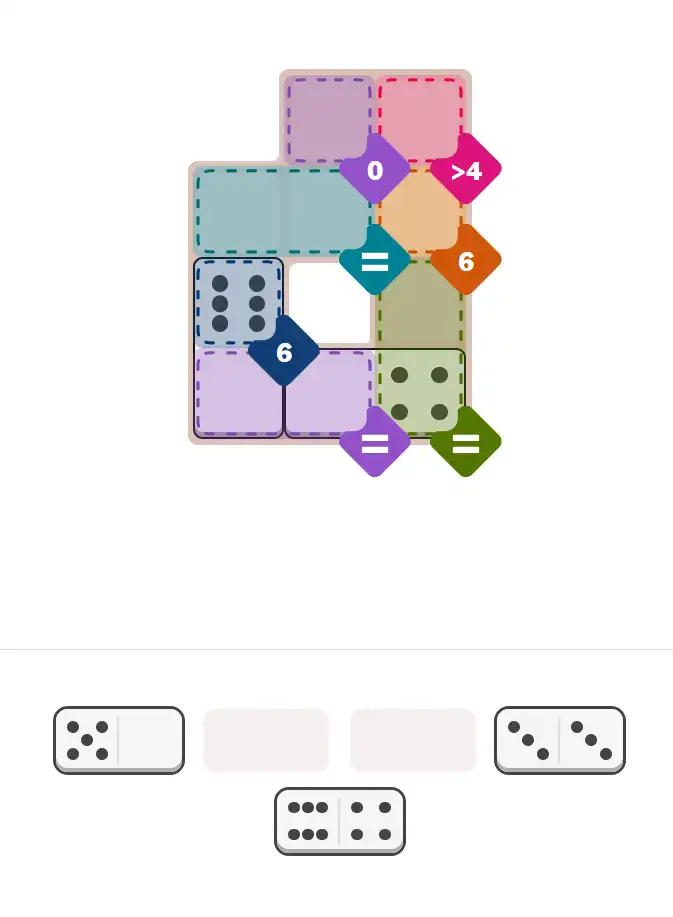
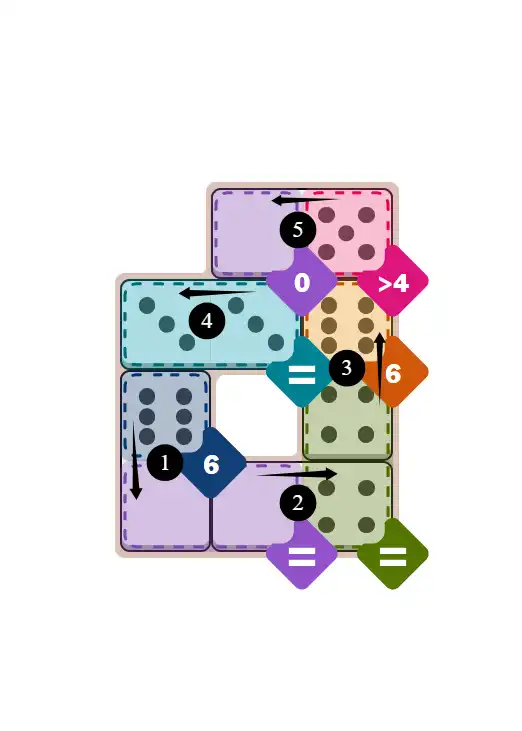
💬 Community Discussion

Leave your comment