NYT Pips Hint, Answer & Solution for December 23, 2025

Dec 23, 2025

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Released on December 23, 2025 (Tuesday), today’s NYT Pips puzzle set—edited by Ian Livengood—offers a crisp, end-of-year logic workout that’s perfect for slowing down, sharpening your focus, and enjoying a thoughtful daily challenge as the holiday season approaches.

Start with Easy #449, constructed by Livengood, where clean sum targets and a generous layout make it ideal for spotting early Pips Hints. This puzzle encourages smooth value tracking, light experimentation, and confidence-building deductions—great for warming up your logic flow without overthinking.

Move into Medium #453, also by Livengood, where the grid tightens and decision-making becomes more deliberate. With extended equals regions, careful comparison rules, and subtle placement traps, this puzzle rewards solvers who pause to map domino distribution and test assumptions before committing to a solution.

Finish with Hard #458 by Rodolfo Kurchan, a deeply layered challenge that showcases expert puzzle design. Unequal regions, multi-cell sums, and interlocking constraints demand full-grid awareness and precise sequencing. Every placement matters here, making each breakthrough feel earned—and memorable.

Whether you’re trading Pips hints, reviewing solution paths, or logging puzzle IDs to track your progress, this December 23 lineup delivers a satisfying balance of structure and creativity. It’s a focused, festive-week challenge that invites careful reasoning, shared insights, and a rewarding logic experience from start to finish.

Written by July

Puzzle Analyst – Nikki

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - Observe

Dominoes Include: [6-4], [6-1], [5-4], [5-1], [3-2], [2-1]. Only 2 domino with 6 pips (6-4, 6-1) for Yellow 12 region.

💡 Hint #1 - Inventory & Dependency Scan

Start by listing all available dominoes and identifying forced values. The Red Equal region can only be satisfied by 6s, and the Light Blue Equal / Blue Equal pair forms a strict dependency: if one is 4 the other must be 2, and vice versa. Lock these relationships early to narrow the search space.

💡 Hint #2 - Anchor the Forced Equal

Use the Red Equal region as an anchor. Since it requires identical values and only one matching domino exists, fixing 6-6 immediately resolves adjacent constraints. This placement also determines valid options for the Yellow <2 and Purple 3 regions through direct pip flow.

💡 Hint #3 - Resolve Linked Equals Chains

Focus on the interdependent Equal regions together. Once Purple <2 forces a 1, the Light Blue Equal must become 4, which in turn forces Blue Equal to be 2. Solving these as a chain prevents trial-and-error and collapses multiple possibilities at once.

💡 Hint #4 - Finish with Remaining Comparisons

With all Equal regions fixed, clean up using the remaining comparison clues. Assign the last dominoes to satisfy Red 5, Light Blue >2, and Green <4 in one pass, confirming that all inequalities are met without conflict.

💡 Hint #1 - Account for rare high and low pips early

Scan the full domino set to identify scarce values. With only one 6 available and limited 0s, lock in regions that require extreme sums first (like >10 or 0) to narrow the solution space quickly.

💡 Hint #2 - Use vertical bridges to satisfy dual constraints

When a domino must connect two regions with different conditions (such as an exact value and an inequality), prioritize vertical placements that satisfy both at once. This often resolves multiple regions with a single move.

💡 Hint #3 - Let singleton values force equal regions

When only one domino remains with a required pip count, use it to force equal regions. This cascades deductions into neighboring regions and reveals exact placements through elimination.

💡 Hint #4 - Resolve large sum regions by full decomposition

For big targets like 10 or >10, break them into all possible component pairs, then eliminate options using already-placed values. Solving these anchors stabilizes the entire grid.

💡 Hint #5 - Finish with inequality cleanup

Leave not-equal regions for last. Once most values are fixed, inequalities become trivial to satisfy, allowing remaining dominoes to fall into place with minimal ambiguity.

🎨 Pips Solver

Dec 23, 2025

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

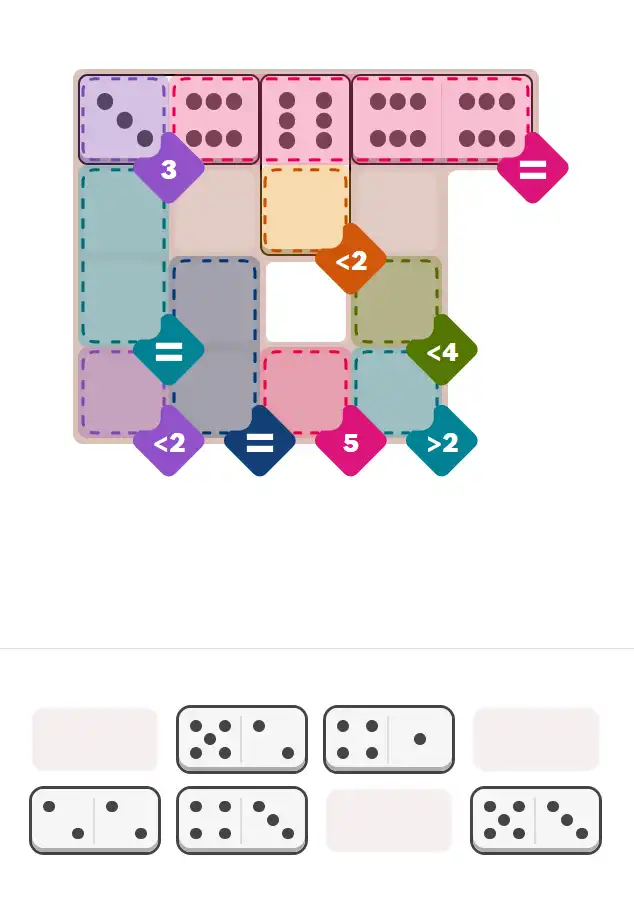
Starting Position & Key First Steps

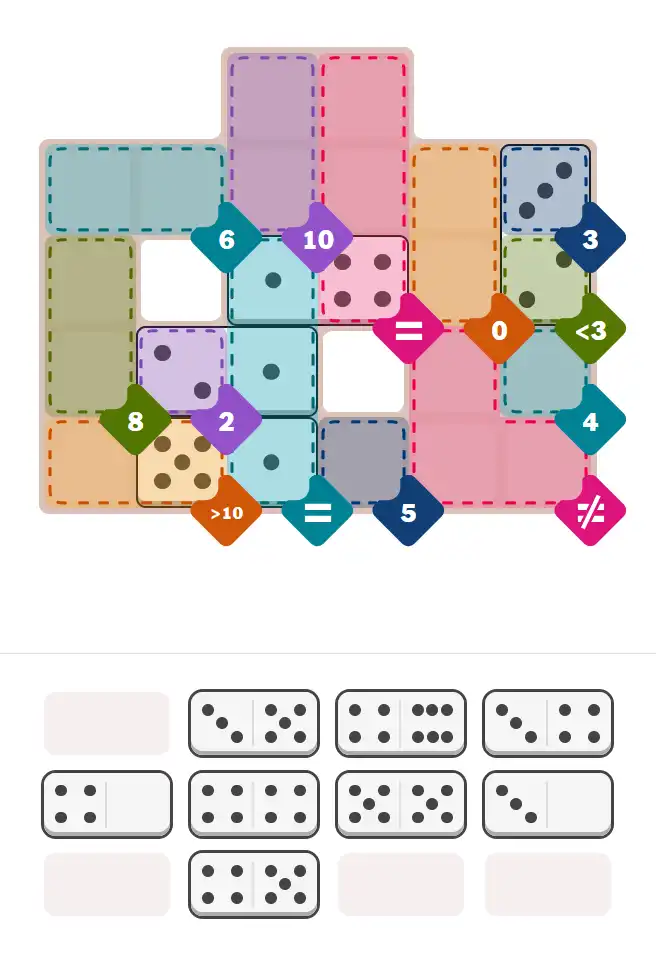
Pips hint for December 23, 2025 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

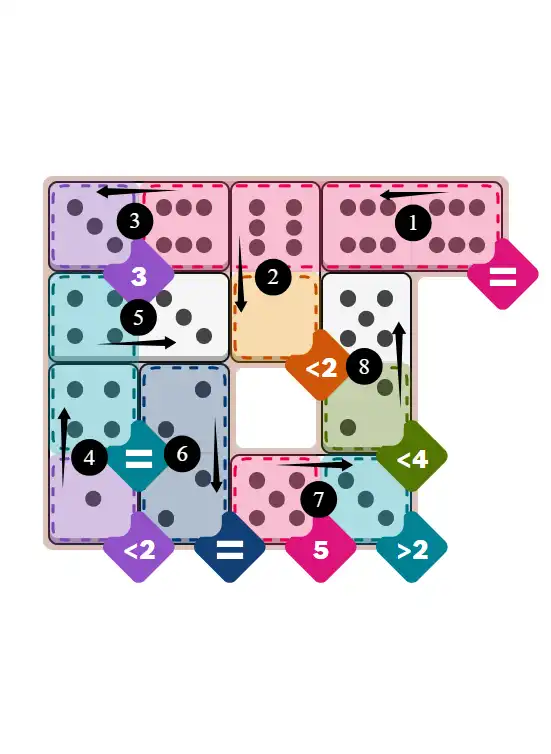
Final Answer: The Solved Grid for Hard Mode

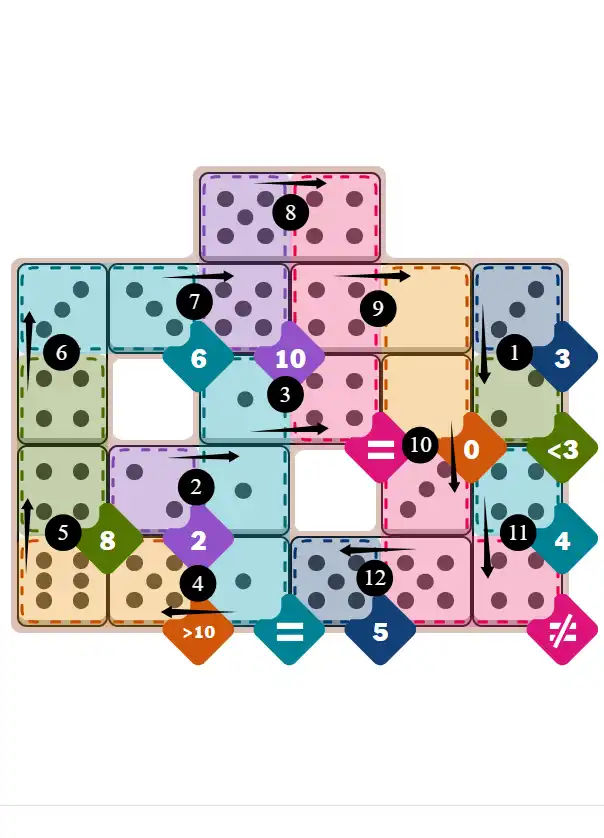
NYT Pips December 23, 2025 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-4], [6-1], [5-4], [5-1], [3-2], [2-1].

2

Step 2: Yellow 12 + Blue 8 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. Only 2 domino with 6 pips (6-4, 6-1). The domino halves in Yellow 12 region must be 6+6. The domino halves in Blue 8 region must be 4+4. The answer is 6-4, placed horizontally; 4-5 (5 up into blank), placed vertically; 6-1 (1 left into blank), placed horizontally.

3

Step 3: Purple 2 + Light Blue 8 + Red 2 --(Arrows ④⑤⑥)

Confirmed by neighboring region and remaining dominoes (5-1, 3-2, 2-1). The domino halves in Light Blue 8 region must be 3+5. The answer is 2-3 (2 into Purple 2 region), placed vertically; 5-1 (1 down into blank), placed vertically; 2-1 (2 into Red 2 region, 1 down into blank), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-6], [6-3], [6-0], [5-3], [5-2], [4-3], [4-1], [2-2]. The domino halves in Red Equal region must be 6. Light Blue Equal and Blue Equal are interdependent: Light Blue Equal=4 ⇔ Blue Equal=2, Light Blue Equal=2 ⇔ Blue Equal=4.

2

Step 2: Red Equal + Yellow <2 + Purple 3 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. Need one domino with the same number placed in Red Equal region, the domino halves in Red Equal region must be 6. The answer is 6-6, placed horizontally; 6-0 (0 into Yellow <2 region), placed vertically; 6-3 (3 into Purple 3 region), placed horizontally.

3

Step 3: Purple <2 + Light Blue Equal + Blue Equal --(Arrows ④⑤⑥)

Confirmed by neighboring region and remaining dominoes (5-3, 5-2, 4-3, 4-1, 2-2). The domino halves in Purple <2 region must be 1. The domino halves in Light Blue Equal region must be 4, therefore, the domino halves in Blue Equal region must be 2. The answer is 1-4, placed vertically; 4-3 (3 right into blank), placed horizontally; 2-2, placed vertically.

4

Step 4: Red 5 + Light Blue >2 + Green <4 --(Arrows ⑦⑧)

Confirmed by neighboring region and remaining dominoes (5-3, 5-2). The answer is 5-3 (5 into Red 5 region, 3 into Light Blue >2 region), placed horizontally; 2-5 (2 into Green <4 region), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-4], [5-5], [5-4], [5-3], [5-1], [4-4], [4-3], [4-1], [4-0], [3-2], [3-0], [2-1]. Only one domino with 6 pips (6-4), the domino halves in Yellow >10 region must be 6+5. The domino halves in Purple 10 region must be 5+5. Only 2 domino halves that contain 0 pips for Yellow 0 region.

2

Step 2: Blue 3 + Green <3 --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. Need one domino placed vertically between Blue 3 region and Green <3 region, the dominoes with 3 pips (5-3, 4-3, 3-2, 3-0). Therefore, the answer is 3-2, placed vertically.

3

Step 3: Purple 2 + Light Blue Equal --(Arrows ②③④)

Confirmed by neighboring region and relative position and remaining dominoes. Only one domino left that with 2 pips (2-1). The domino halves in Light Blue Equal region must be 1. The answer is 2-1 (2 into Purple 2 region), placed horizontally; 1-4 (4 into Red Equal region), placed horizontally; 1-5 (5 into Yellow >10 region), placed horizontally.

4

Step 4: Yellow >10 + Green 8 + Light Blue 6 + Purple 10 + Red Equal --(Arrows ⑤⑥⑦⑧⑨)

Confirmed by neighboring region and remaining dominoes (6-4, 5-5, 5-4, 5-3, 4-4, 4-3, 4-0, 3-0). The domino halves in Yellow >10 region must be 6+5. The domino halves in Green 8 region must be 4+4. The domino halves in Light Blue 6 region must be 3+3. The domino halves in Purple 10 region must be 5+5. The domino halves in Red Equal region must be 4. The answer is 6-4 (6 into Yellow >10 region), placed vertically; 4-3, placed vertically; 3-5, placed horizontally; 5-4, placed horizontally; 4-0 (0 into Yellow 0 region), placed horizontally.

5

Step 5: Red Not Equal + Yellow 0 + Light Blue 4 + Blue 5 --(Arrows ⑩⑪⑫)

Confirmed by neighboring region and remaining dominoes (5-5, 4-4, 3-0). The domino halves in Red Not Equal region must be different. The answer is 0-3 (0 into Yellow 0 region, the Yellow 0 region done), placed vertically; 4-4 (one 4s into Light Blue 4 region), placed vertically; 5-5 (one 5s into Blue 5 region), placed horizontally.

🎥 NYTpips Quick Strategy ⚡ Key Logic & Entry-Exit Signals

Unlock concise NYTpips strategy in this fast-paced

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for December 26, 2025

View Answer →

NYT Pips Hints & Answers for December 25, 2025

View Answer →

NYT Pips Hints & Answers for December 24, 2025

View Answer →

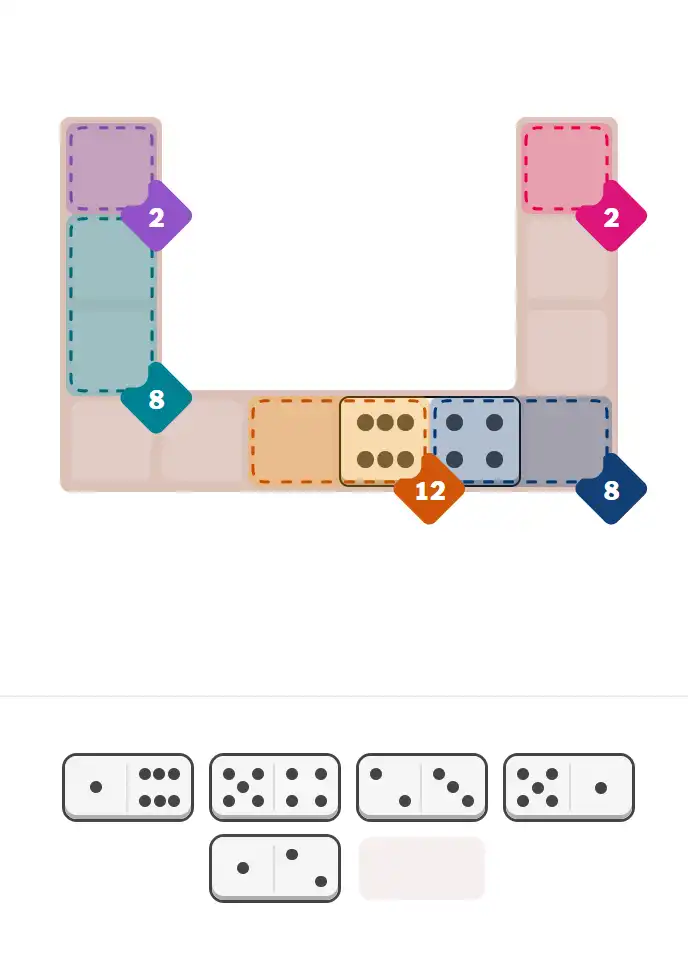
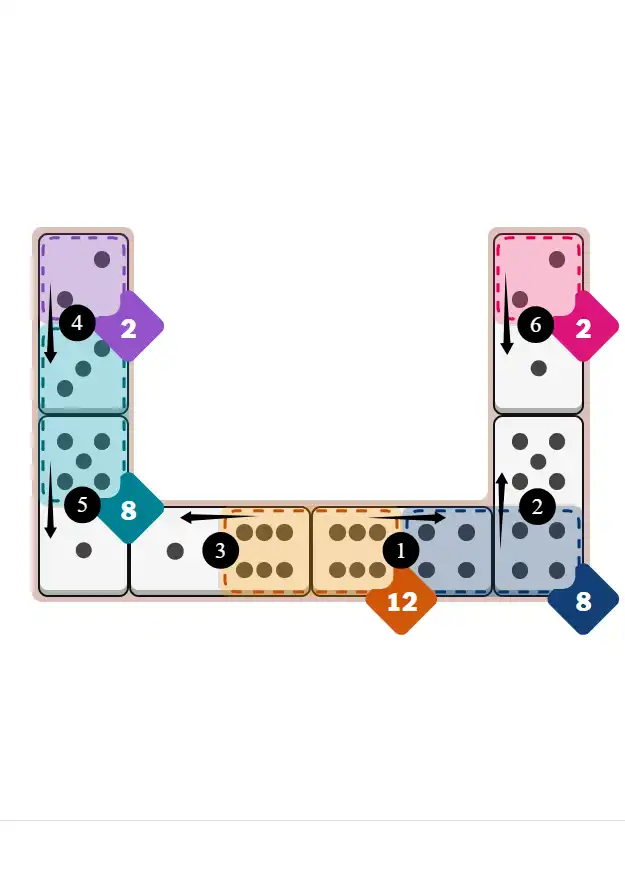
💬 Community Discussion

Leave your comment