NYT Pips Hint, Answer & Solution for December 19, 2025

Dec 19, 2025

🚨 SPOILER WARNING

This page contains the final **answer** and the complete **solution** to today's NYT Pips puzzle. If you haven't attempted the puzzle yet and want to try solving it yourself first, now's your chance!

Click here to play today's official NYT Pips game first.

Want hints instead? Scroll down for progressive clues that won't spoil the fun.

🎲 Today's Puzzle Overview

Released on December 19, 2025 (Friday), today’s NYT Pips puzzles—edited by Ian Livengood—set a relaxed, end-of-week rhythm that’s perfect for slowing down, comparing notes, and solving side by side with the community.

Start the session with Easy #425, constructed by Livengood, where approachable sum targets, friendly equals regions, and thoughtfully placed empty cells create an ideal warm-up. This grid is great for spotting early patterns, trading quick Pips Hints, and building confidence together before the logic tightens.

Move into Medium #429, also by Livengood, and feel the discussion naturally deepen. Stacked equals zones and clean sum logic invite solvers to pause, explain reasoning, and compare alternative solution paths—exactly the kind of puzzle that rewards shared analysis and careful constraint reading.

Wrap up the week with Hard #436, crafted by Rodolfo Kurchan, a satisfying Friday challenge filled with layered sum regions and interlocking constraints. This is the puzzle where teamwork shines: testing ideas, revisiting assumptions, and celebrating that collective “aha” when the final placements click.

Share your solution routes, swap detailed Pips Hint strategies, and enjoy this December 19, 2025 release as a communal NYT Pips experience—designed for conversation, learning, and a rewarding finish to the puzzle week.

Written by Ander

Puzzle Analyst – Lucas

💡 Progressive Hints

Try these hints one at a time. Each hint becomes more specific to help you solve it yourself!

💡 Hint #1 - So easy

Do it.

💡 Hint #1 - Zero Inventory Scan

Begin by counting how many domino halves contain 0 pips. When an Equal region depends on a single value, a limited zero supply immediately narrows the possible outcome and frames the entire solve.

💡 Hint #2 - Forced Sum Resolution

If a target sum cannot be formed by any single domino, resolve it through value pairing. Identifying the only available pip (here, the lone 3) forces the remaining halves and locks neighboring regions simultaneously.

💡 Hint #3 - Equal Region Collapse

Once surrounding constraints are satisfied, large Equal regions often collapse to the lowest remaining pip. After higher values are consumed, zeros naturally fill the Equal space without ambiguity.

💡 Hint #4 - Cascading Equals Logic

When multiple Equal and Sum regions touch, solve them as a chain. Fixing one Equal value restricts adjacent sums, allowing several regions to resolve in a single logical cascade rather than isolated guesses.

💡 Hint #1 - Pip Inventory Scan

Start by counting scarce pip values across the full domino set. With only three dominoes containing 4 pips available, immediately reserve one for the Red 4 region. Early inventory prevents downstream conflicts and narrows viable placements.

💡 Hint #2 - Zero Lock-In via Scarcity

When only a single 0 pip exists, its placement becomes forced. Use that certainty to resolve adjacent sum regions simultaneously, converting one fixed placement into multiple confirmed values without guessing.

💡 Hint #3 - Equal-by-Elimination

When a small sum region depends on limited pip values, eliminate impossibilities instead of searching combinations. Here, remaining 1-pips force the Light Blue region to resolve as 1+1, while also fixing the Red 4 region allocation.

💡 Hint #4 - High-Sum Pair Commitment

Large sum targets often collapse into a single viable pair once medium values are consumed elsewhere. After reserving the needed 4, the Purple 10 region can only be satisfied by a double-5, making this a clean, confidence placement.

💡 Hint #5 - Triple-Pip Saturation

When a region requires repeated values, check whether the domino set supports full saturation. The Blue 6 and Yellow 9 regions resolve cleanly once you recognize they must be built entirely from identical pip values.

💡 Hint #6 - Residual Pair Resolution

Late-game medium sums are best solved by matching leftover pip pairs. With limited options remaining, the Purple 3 region resolves naturally as 1+2, while the Red 4 region finally locks its reserved value.

💡 Hint #7 - Deferred Sum Closure

Some regions are best solved after neighboring constraints mature. Returning to the Green 7 region once its supporting values are fixed allows a simple 4+3 confirmation without rework.

💡 Hint #8 - Final Domino Placement

In the endgame, placement becomes mechanical rather than logical. With all constraints satisfied and only one domino left, orientation is fixed and the grid resolves without ambiguity.

🎨 Pips Solver

Dec 19, 2025

Click a domino to place it on the board. You can also click the board, and the correct domino will appear.

✅ Final Answer & Complete Solution For Hard Level

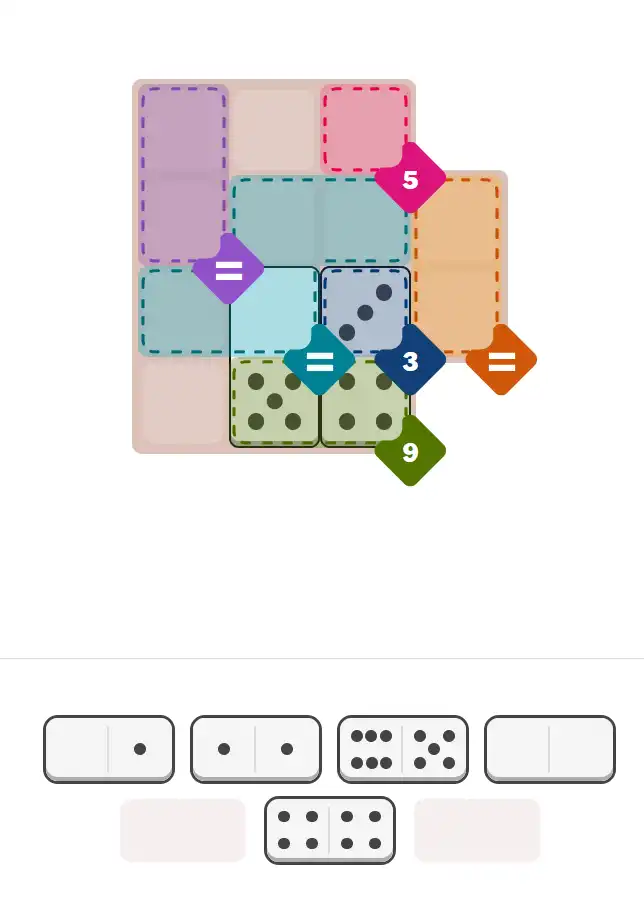
The key to solving today's hard puzzle was identifying the placement for the critical dominoes highlighted in the starting grid. Once those were in place, the rest of the puzzle could be solved logically. See the final grid below to compare your solution.

Starting Position & Key First Steps

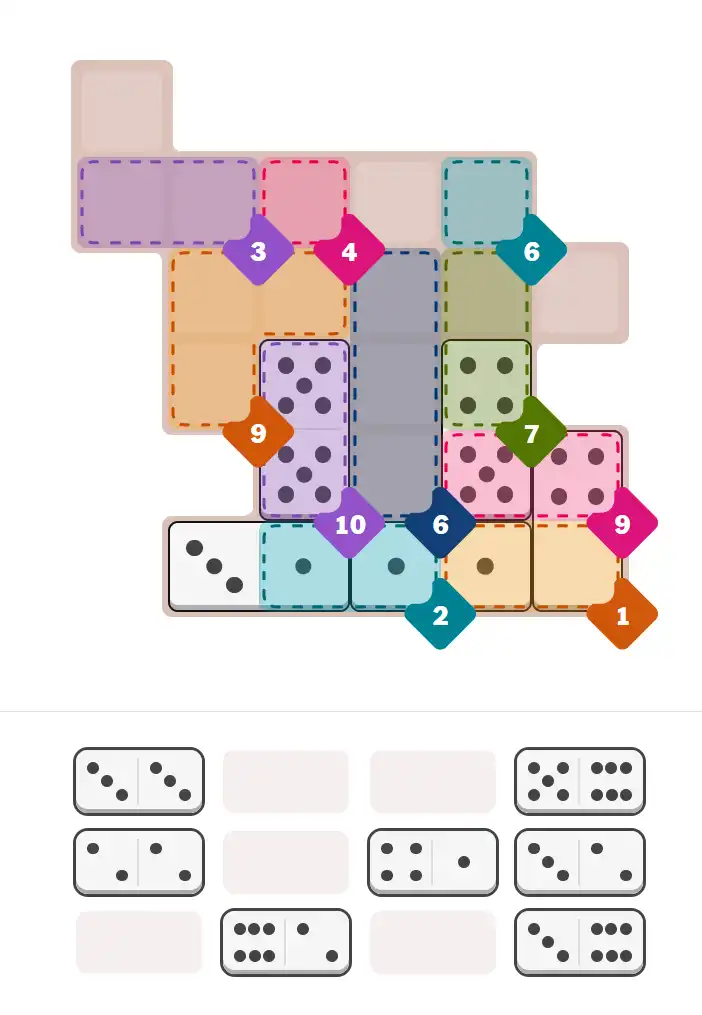
Pips hint for December 19, 2025 – hard level puzzle grid with critical first placements and strategy

This image shows the initial puzzle grid for the hard level, with a few critical first placements highlighted.

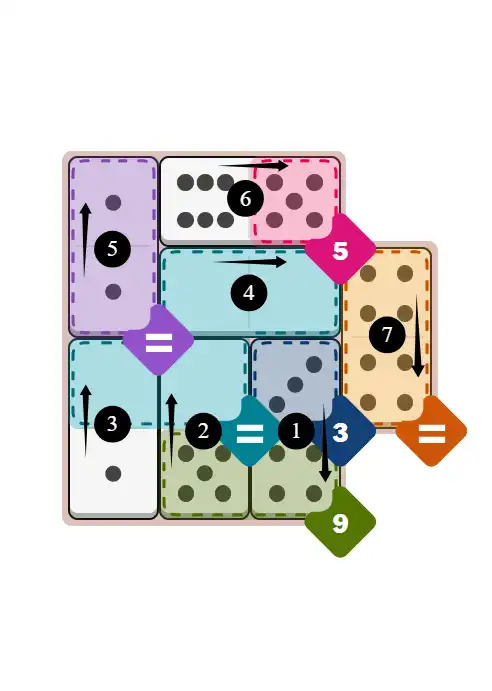
Final Answer: The Solved Grid for Hard Mode

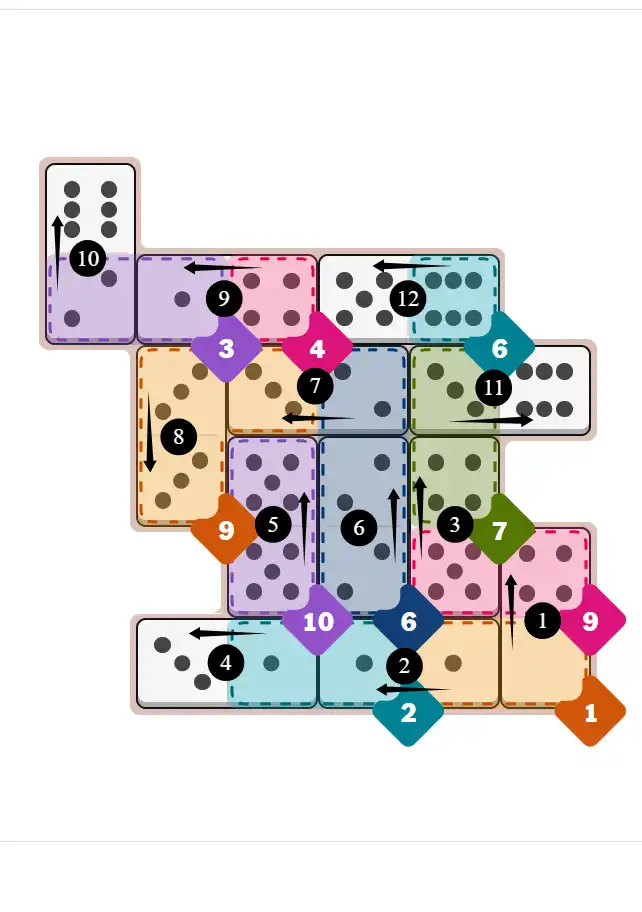
NYT Pips December 19, 2025 hard puzzle full solution grid showing final answer with hints

Compare this final grid with your own solution to see the correct placement of all dominoes.

🔧 Step-by-Step Answer Walkthrough For Easy Level

1

Step 1

Dominoes Include: [6-6], [6-4], [6-0], [5-3], [3-0].

2

Step 2: Blue 12 --(Arrows ①)

Confirmed by neighboring region and step 1 and relative position. The answer is 6-6, placed vertically.

3

Step 3: Purple 5 + Light Blue Equal --(Arrows ②③)

Confirmed by neighboring region and remaining dominoes (6-4, 6-0, 5-3, 3-0). The domino halves in Light Blue Equal region must be 3. The answer is 5-3 (5 into Purple 5 region), placed vertically; 3-0 (0 right into blank), placed horizontally.

4

Step 4: Red 0 + Yellow <5 --(Arrows ④⑤)

Confirmed by neighboring region and remaining dominoes (6-4, 6-0). The answer is 0-6 (6 down into blank), placed vertically; 4-6 (4 into Yellow <5 region, 6 left into blank), placed horizontally.

🔧 Step-by-Step Answer Walkthrough For Medium Level

1

Step 1

Dominoes Include: [6-5], [5-0], [4-4], [4-3], [1-1], [1-0], [0-0]. Only 4 domino halves that contain 0 pips for Light Blue Equal region.

2

Step 2: Blue 3 + Green 9 --(Arrows ①②)

Confirmed by neighboring region and step 1 and relative position. No domino sum to be 9. Only one domino with 3 pips (4-3). The domino halves in Green 9 region must be 4+5. The answer is 3-4 (3 into Blue 3 region), placed vertically; 5-0 (0 into Light Blue Equal region), placed vertically.

3

Step 3: Light Blue Equal --(Arrows ③④)

Confirmed by neighboring region and relative position and remaining dominoes (6-5, 4-4, 1-1, 1-0, 0-0). The domino halves in Light Blue Equal region must be 0. The answer is 1-0 (1 down into blank), placed vertically; 0-0, placed horizontally.

4

Step 4: Purple Equal + Red 5 + Yellow Equal --(Arrows ⑤⑥⑦)

Confirmed by neighboring region and remaining dominoes (6-5, 4-4, 1-1). The domino halves in Light Blue Equal region must be 0. The answer is 1-1 (Purple Equal region), placed vertically; 6-5 (6 into blank, 5 into Red 5 region), placed horizontally; 4-4 (Yellow Equal region), placed vertically.

🔧 Step-by-Step Answer Walkthrough For Hard Level

1

Step 1

Dominoes Include: [6-5], [6-3], [6-2], [5-5], [5-4], [4-1], [4-0], [3-3], [3-2], [3-1], [2-2], [1-1]. Only 3 domino with 4 pips (5-4, 4-1, 4-0), need one for Red 4 region.

2

Step 2: Yellow 1 + Red 9 --(Arrows ①②③)

Confirmed by neighboring region and step 1 and relative position. Only one domino with 0 pips (4-0). The domino halves in Yellow 1 region must be 0+1. The domino halves in Red 9 region must be 4+5. The answer is 0-4, placed vertically; 1-1 (one 1s into Light Blue 2 region), placed horizontally; 5-4 (4 into Green 7 region), placed vertically (can't placed horizontally, confirmed by not more enough 1 pips for Blur 6 region).

3

Step 3: Light Blue 2 --(Arrows ④)

Confirmed by neighboring region and step 2 and remaining dominoes with 1 pips (4-1, 3-1). The domino halves in Light Blue 2 region must be 1+1. Only one domino left that contain 4 pips (4-1) for Red 4 region. The answer is 1-3 (3 left into blank), placed horizontally.

4

Step 4: Purple 10 --(Arrows ⑤)

Confirmed by neighboring region and remaining dominoes (6-5, 6-3, 6-2, 5-5, 4-1, 3-3, 3-2, 2-2). 4 pips must placed in Red 4 region, Therefore, the domino halves in Purple 10 region must be 5+5. The answer is 5-5 (whole domino), placed vertically.

5

Step 5: Blue 6 + Yellow 9 --(Arrows ⑥⑦⑧)

Confirmed by neighboring region and relative position and remaining dominoes (6-5, 6-3, 6-2, 4-1, 3-3, 3-2, 2-2). The domino halves in Blue 6 region must be 2+2+2. The domino halves in Yellow 9 region must be 3+3+3. The answer is 2-2 (whole domino), placed vertically; 2-3, placed horizontally; 3-3 (whole domino), placed vertically.

6

Step 6: Red 4 + Purple 3 --(Arrows ⑨⑩)

Confirmed by neighboring region and remaining dominoes (6-5, 6-3, 6-2, 4-1). The domino halves in Purple 3 region must be 1+2. The answer is 4-1 (4 into Red 4 region), placed horizontally; 2-6 (6 up into blank), placed vertically.

7

Step 7: Green 7 --(Arrows ⑪)

Confirmed by neighboring region and step 2 and remaining dominoes (6-5, 6-3). The domino halves in Green 7 region must be 4+3. The answer is 3-6 (6 right into blank), placed horizontally.

8

Step 8: Light Bule 6 --(Arrows ⑫)

The answer is 6-5 (5 left into blank), placed horizontally.

🎥 NYTpips Quick Strategy ⚡ Entry & Exit Logic for Smarter Moves

Pay attention to the trigger points — these subtle logic cues make all the difference

💡 Pro Tips for Similar Puzzles

Start with Constraints

Always begin with the most constrained regions - sum regions with small numbers or tight spaces.

Use Equal Regions

Use "equal" regions as anchors - they eliminate many possibilities quickly.

Work Systematically

Let the rules guide your placement rather than guessing randomly.

Double-Check

Verify each region's rules are satisfied before moving to the next.

🎓 Keep Learning & Improve

🧠 Strategy Guide

Master the core techniques to solve any Pips puzzle, no matter the difficulty.

🎮 How to Play

New to Pips? Learn all the rules and conditional regions in minutes.

📖 More to Read

NYT Pips Hints & Answers for December 22, 2025

View Answer →

NYT Pips Hints & Answers for December 21, 2025

View Answer →

NYT Pips Hints & Answers for December 20, 2025

View Answer →

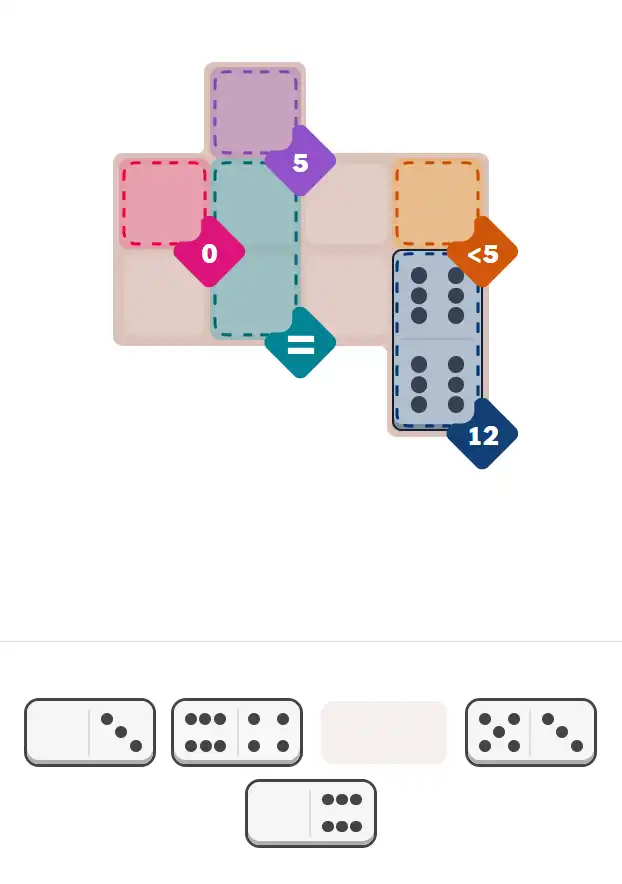
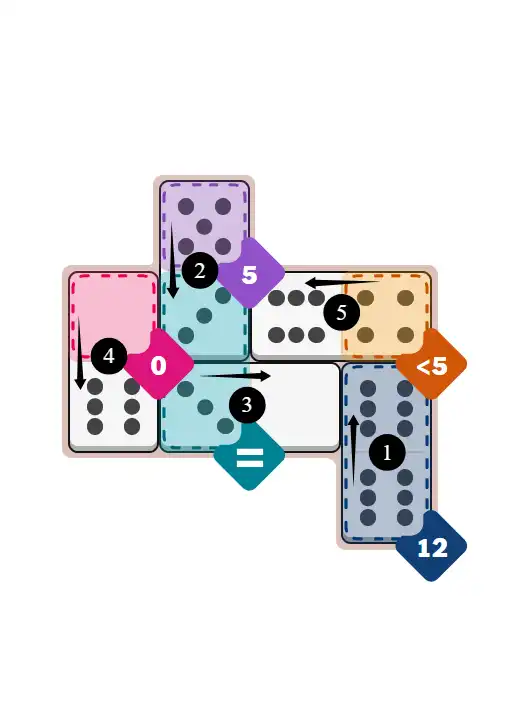
💬 Community Discussion

Leave your comment